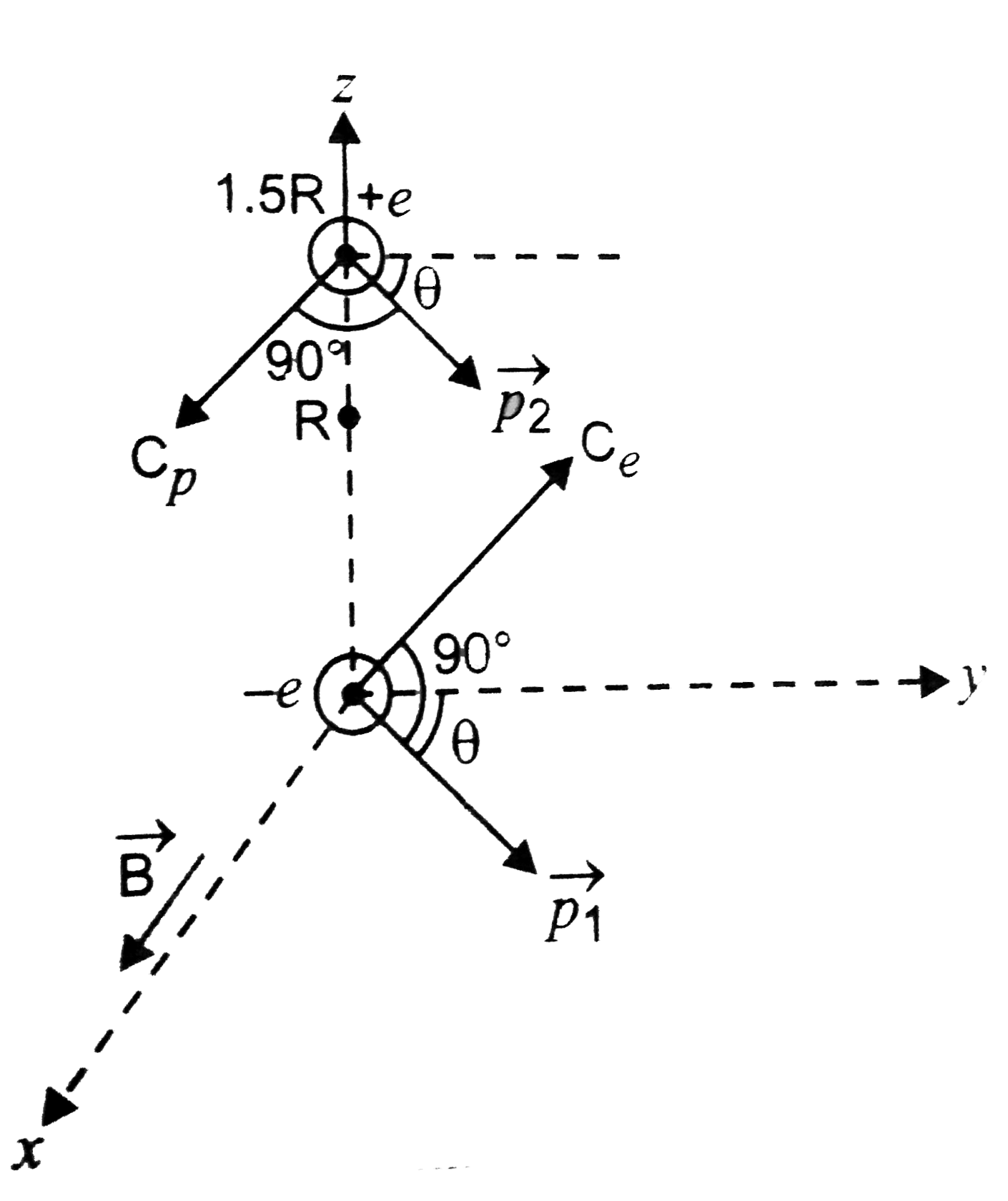
Here, `vecB(=B_0hati)` is acting along the x-axis. For a circular orbit, the momentum of the electron and position are in y-z plane. Let `vecp_1` and `vecp_2` be the momentum of the electron and position respectively. Both of them due to same momentum `(=eBR)` move on circular orbits, each of radius R, but in opposite sense.
Let `vecp_1` make an angle `theta` with the y-axis and `vecp_2` must make the same angle `theta` with y-axis. The centres of the respective circular orbits must be perpendicular to the momenta at a distance R. Let the centre of the circular orbit of the electron be at `C_e` and of the position be at `C_p`.
The coordinates of `C_e` is `(0, R sin theta, R cos theta)`
The coordinates of `C_p` is `[0, -Rsin theta, (3/2R-Rcos theta)]`
The two circular orbits will not intersect if the distance between their two centre is greater than 2R.
Let d be the distance between `C_p` and `C_e`. Then
`d^2=[-Rsintheta-(Rsintheta)]^2+[(3/2R-Rcostheta)-(Rcostheta)]^2`
`=4R^2sin^2theta+9/4R^2-6R^2costheta+4R^2cos^2theta=4R^2(sin^2theta+cos^2theta)+9/4R^2-6R^2costheta`
`=25/4R^2-6R^2costheta`
The two circular orbits will not intersect each other if `dgt2R` or `d^2gt4R^2`
`:. 25/4R^2-6R^2costhetagt4R^2` or `25/4-6costhetagt4` or `9/4gt6costheta` or `cos thetalt3//8`