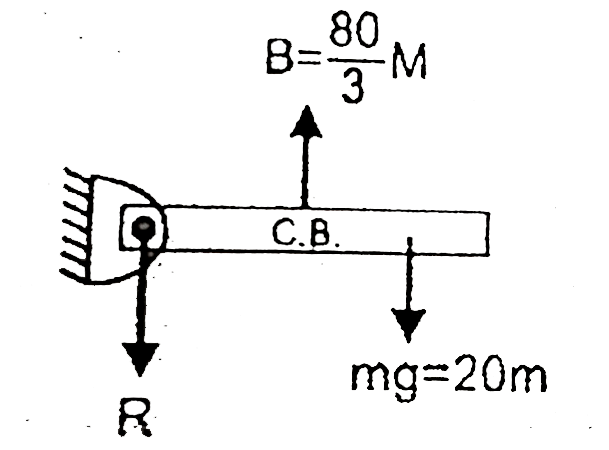
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A rod of mass m = 2kg, length l = 1m, has uniform cross-section area A...
Text Solution
|
- A rod of uniform cross-section of mass M and length L is hinged about ...
Text Solution
|
- A uniform rod AB of mass 2 kg is hinged at one end A. The rod is kept ...
Text Solution
|
- A hollow sphere of mass M = 50 kg and radius r=(3/(40pi))^(1//3)m is i...
Text Solution
|
- A rod of mass m = 2kg , length l = 1m , has uniform cross-section area...
Text Solution
|
- A tube of small uniform cross section is used to siphon the water from...
Text Solution
|
- A thin uniform copper rod of length l and cross-section area A and mas...
Text Solution
|
- The pressure at a point in water is 10 N//m^(2). The depth below this ...
Text Solution
|
- Water enters a horizontal pipe of non uniform cross section with a vel...
Text Solution
|