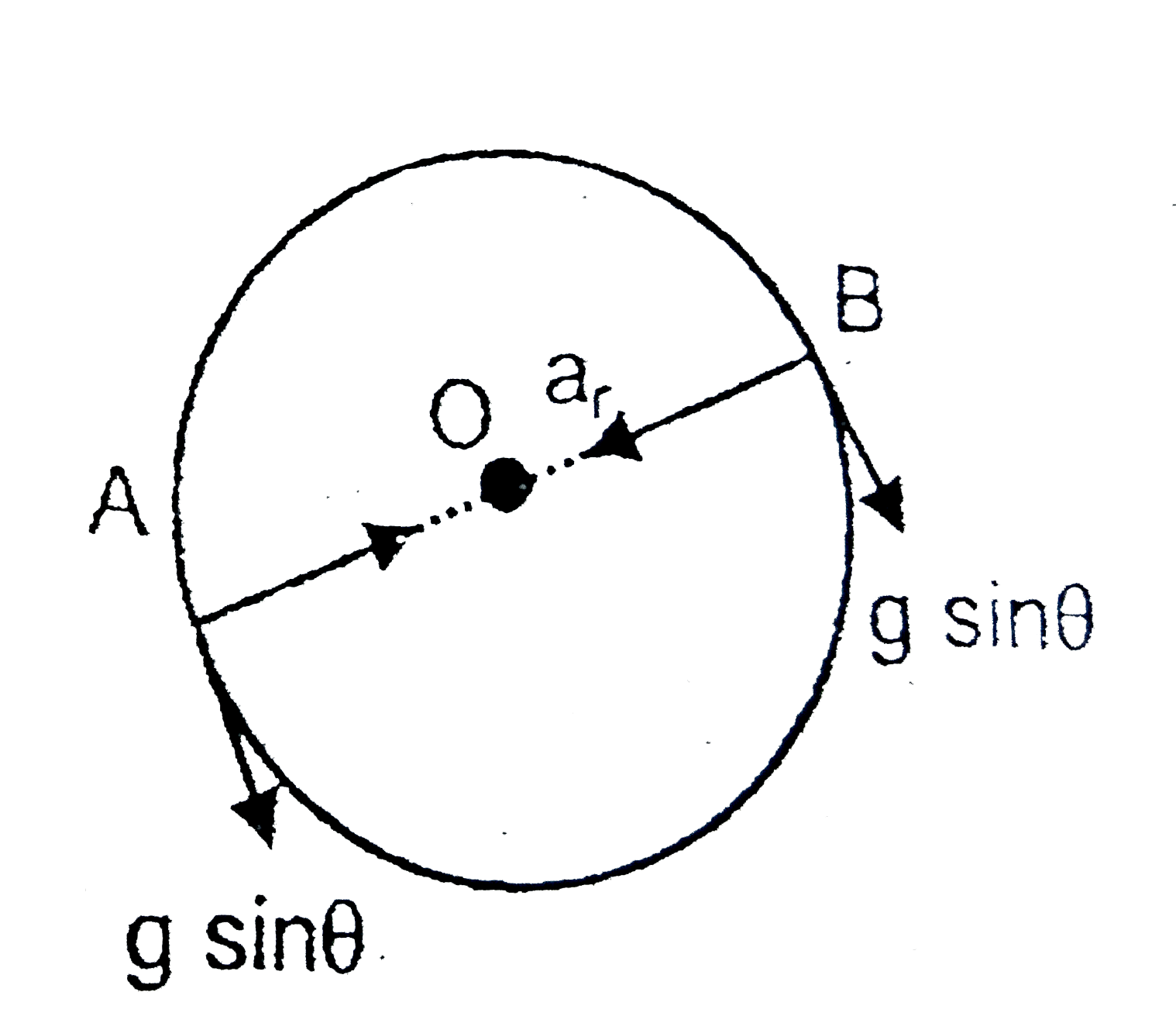A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle of mass m oscillates inside the smooth surface a fixed pipe...
Text Solution
|
- A charged particle moves insides a pipe which is bent as shown in Fig....
Text Solution
|
- A particle of mass m oscillates along the horizontal diameter AB insi...
Text Solution
|
- A particle of mass m oscillates inside the smooth surface a fixed pipe...
Text Solution
|
- A particle of mass m oscillates inside a smooth spherical shell of rad...
Text Solution
|
- A heavy particle of mass m is in motion on a smooth surface of hemisph...
Text Solution
|
- R त्रिज्या के एक स्थिर एंव चिकने गोले पर m द्रव्यमान का एक कण पकड़कर र...
Text Solution
|
- IF a particle of mass m is moving in a horizontal circle of r...
Text Solution
|
- The kinetic energy K of a particle moving along x - axis varies its po...
Text Solution
|