Home
Class 12
PHYSICS
A triangular medium has varying refracti...

A triangular medium has varying refracting index `mu = mu_(0) + ax` where x is the distance (in cm) along x-axis from origin and `m_(0) = 4//3`. A ray is incident normally on face OA at the mid-point of OA. Find the range of value of a so that light does not escape through face AB when it falls first time on the face AB.

Text Solution

Verified by Experts

The correct Answer is:
`a gt (2)/(9)`
Promotional Banner

Topper's Solved these Questions

  • GEOMETRICAL OPTICS

    ARIHANT|Exercise Level 2|62 Videos

  • GEOMETRICAL OPTICS

    ARIHANT|Exercise Level 3|9 Videos

  • ELECTROSTATICS

    ARIHANT|Exercise Level 3|59 Videos

  • MAGNETIC EFFECT OF CURRENT

    ARIHANT|Exercise Magnetic effect of Current|45 Videos

Similar Questions

Explore conceptually related problems

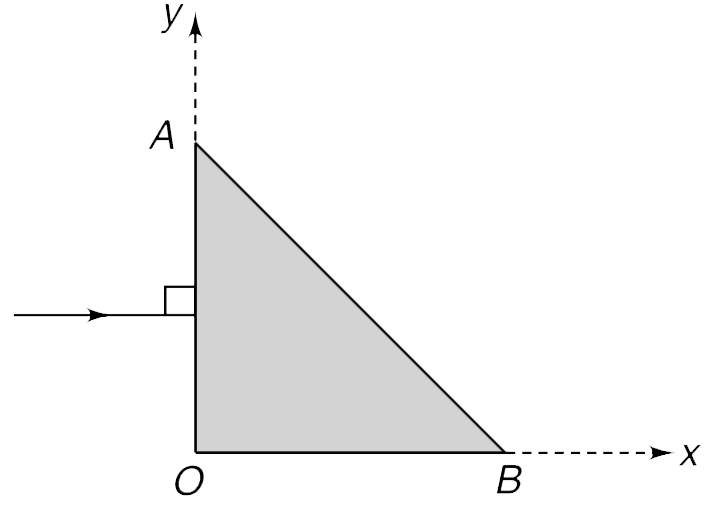
A triangular medium has varying refracting index n=n_0 +ax , where x is the distance (in cm) along x-axis from origin and n_0 = 4/3 . A ray is incident normally on face OA at the mid-point of OA. The range of a so that light does not escape through face AB when it falls first time on the face AB(OA=4cm, OB=3cm and AB=5cm): (Surrounding medium is air)

In figure, parallel beam of light is incident on the plane of the slits of a Young's double-slit experiment. Light incident on the slit S_(1) passes through a medium of variable refractive index mu = 1 + ax (where 'x' is the distance from the plane of slits as shown), up to distance 'I' before falling on S_(1) . Rest of the space is filled with air. If at 'O' a minima is formed. then the minimum value of the positive constant a (in terms of l and wavelength lambda in air) is

An equilateral prism ABC is placed in air with its base side BC lying horizontally along x-axis as shown in the figure. A ray given by sqrt(3)z +x=10 is incident at a point P on the face AB of the prism (a) Find the value mu from which the ray grazes the face AB (b) Find the direction of the initially refracted ray if mu = (3)/(2) (c) Find the equation of ray coming out of the prism if bottom BC is silvered ?

A ray of light enters the face AB of a glass prism of refractive index mu at an angle of incidence i . Find the value of i such that no ray emerges from the face AC of the prism, given angle of prism is A .

A ray of light the face AB of a glass prism of refractive index mu at an angle of incidence i . Find the value of i such that no ray emerges from the face AC of the prism. Given angle of prism is A .

The refractive index of a medium changes as mu=mu_(0)[1-(x^(2)+y^(2))/(d_(2))]^(1//2) where mu_(0) is the refractive index on the z axis. A plane wavefront (AB) is incident along z axis as shown in the figure. Draw the wavefront at a later time Deltat . Is the wavefront getting focused?

A parallel beam of light travelling in x direction is incident on a glass slab of thickness t. The refractive index of the slab changes with y as mu = mu_(0) ( 1 – ( y2) /( y_(2)^( 0) ) ) where mu_(0) is the refractive index along x axis and y_(0) is a constant. The light beam gets focused at a point F on the x axis. By using the concept of optical path length calculate the focal length f. Assume f gtgt t and consider y to be small.

Two plane mirrors M1 and M2 , placed at right angles, form two sides of a container. Mirror M1 is inclined at an angle theta_(0) to the horizontal. A light ray AB is incident normally on M1 . Now the container is filled with a liquid of refractive index mu so that the ray is first refracted, then reflected at M1 . The ray is next reflected at M2 and then comes out of the liquid surface making an angle theta with the normal to the liquid surface. Find theta .

Two identical equilat- eral glass (refractive index = sqrt(2)) prisms ABC and CDE are kept such that the angle between faces AC and CE is q. A ray of light is incident at an angle i at the face AB and traverses through the two prisms along the path PQRSTU. Find the value of angle i and theta such that angle between the incident ray PQ and emergent ray TU is minimum.