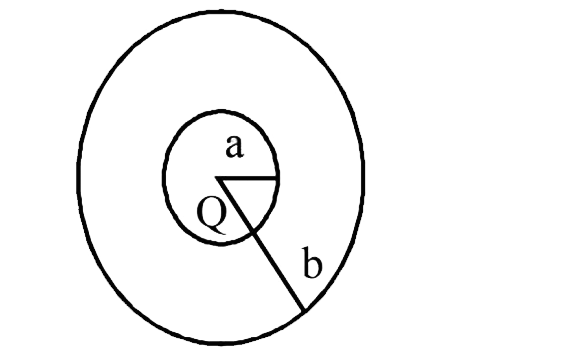
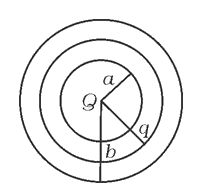
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The region between two concentric spheres of radii 'a' and 'b', respec...
Text Solution
|
- The region between two concentric spheres of radii 'a' and 'b', respec...
Text Solution
|
- त्रिज्या a तथा b के दो संकेन्द्री गोले के बीच के स्थान में आयतन आवेश घ...
Text Solution
|
- A system consits of a uniformly charged sphere of radius R and a surro...
Text Solution
|
- An insulating solid sphere of the radius R is charged in a non - unifo...
Text Solution
|
- An insulating solid sphere of the radius R is charged in a non - unifo...
Text Solution
|
- Charge density of a sphere of radius R is rho = rho0/r where r is dist...
Text Solution
|
- The region between two concentric spheres of radii 'a' and 'b', respec...
Text Solution
|
- The region between two concentric spheres of radii 'a' and 'b', respec...
Text Solution
|