A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Conisder an electric field vecE=E0hatx where E0 is a constant . The ...
Text Solution
|
- Conisder an electric field vecE=E0hatx where E0 is a constant . The fl...
Text Solution
|
- Calculate the total electric flux through the paraboloidal surface due...
Text Solution
|
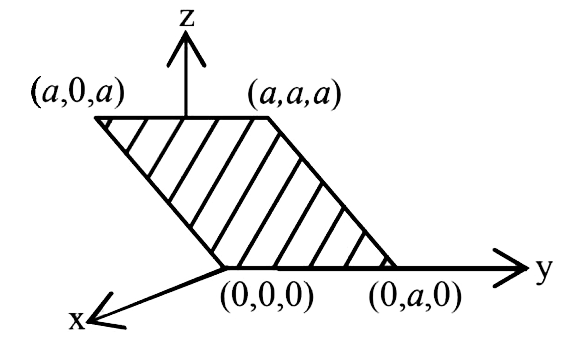
- Find the area of the shaded field shown in figure.
Text Solution
|
- Electric flux in an electric field vecE through area vector vec(ds) is...
Text Solution
|
- What will be the electric flux passing through the area vecS=10hati pl...
Text Solution
|
- a भुजा वाले एक घन को एक विधुत क्षेत्र vecE =c x hati (जहाँ c धनात्मक व...
Text Solution
|
- Find the area of the shaded field shown in figure.
Text Solution
|
- आकृति 11.8 में दर्शाये गये छायांकित खेत का क्षेत्रफल ज्ञात कीजिए।
Text Solution
|