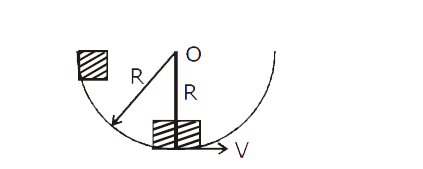
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A block of mass m slides down along the surface of the bowl from the r...
Text Solution
|
- A 0.098-kg block slides down a frictionless track as shown in (Fig. )....
Text Solution
|
- All surfaces are smooth Find the horizontal displacements of the block...
Text Solution
|
- A block of mass m is placed on a triangular block of mass M(M = 2m) , ...
Text Solution
|
- A block of mass M slides down a rough inclined surface of inclination ...
Text Solution
|
- द्रव्यमान m की एक वस्तु त्रिज्या R वाले अर्द्धगोलीय प्याले के धरातल पर...
Text Solution
|
- A block of mass m slides down along the surface of the bowl from the r...
Text Solution
|
- All surfaces are smooth. Find the horizontal displacements of the bloc...
Text Solution
|
- All surfaces are smooth. Find the horizontal displacements of the bloc...
Text Solution
|