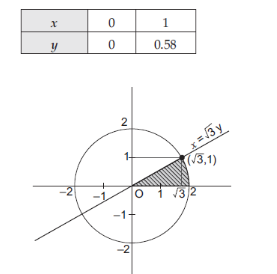
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Prove that the area in the first quadrant enclosed by the axis, the ...
Text Solution
|
- Find the area of the region in the first quadrant enclosed by x-a xi s...
Text Solution
|
- प्रथम चतुर्थांश में वृत्त x^(2)+y^(2)=4, रेखा x=sqrt(3)y एवं x-अक्ष द...
Text Solution
|
- प्रथम चतुर्थांश में वृत्त x^(2) + y^(2) = 4 रेखा x =sqrt(3)y एव X -...
Text Solution
|
- Find the area of the region in the first quadrant enclosed by X-axis a...
Text Solution
|
- The area in the first quadrant enclosed by the axis, the line x=ysqrt(...
Text Solution
|
- The area in the first quadrant enclosed by the axes, the line x=y sqrt...
Text Solution
|
- Find the area of the region in the first quadrant enclosed by x-axis,...
Text Solution
|
- Find the area of the region in the first quadrant enclosed by x-axis, ...
Text Solution
|