Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
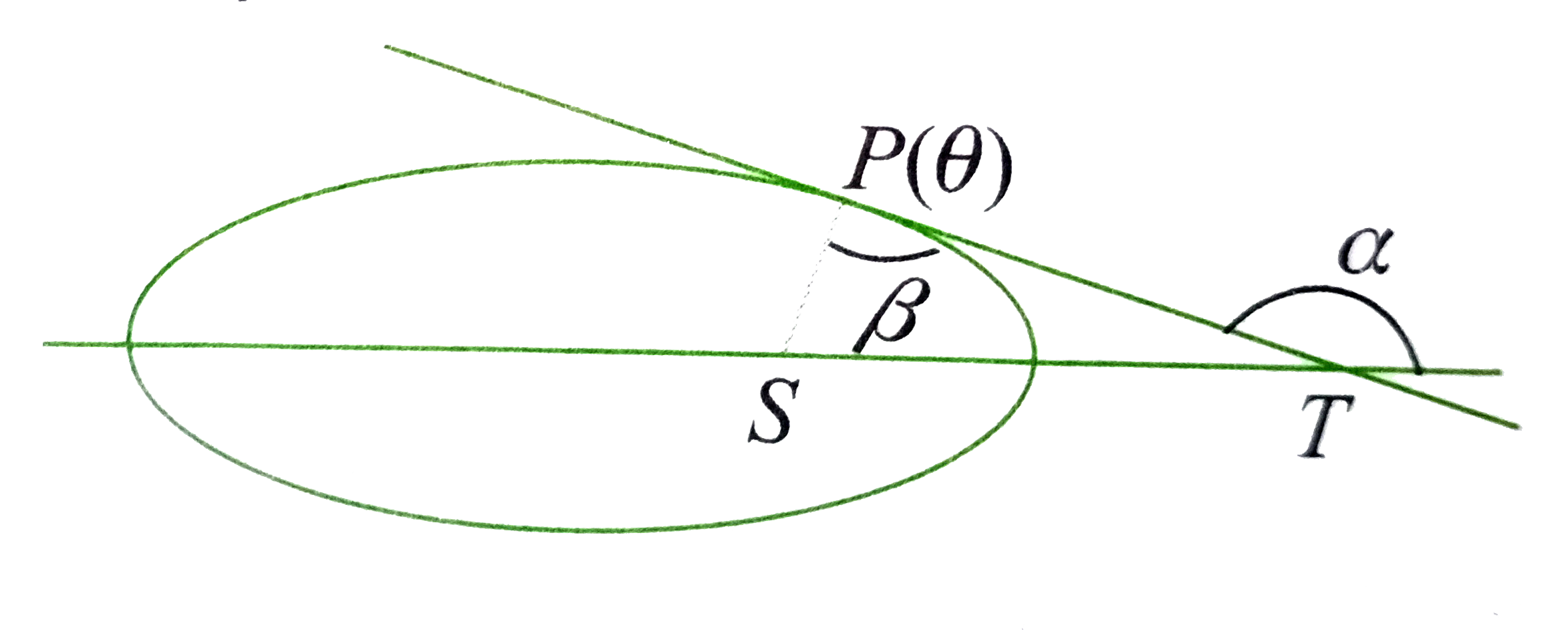
- If the tangent at any point of the ellipse (x^2)/(a^3)+(y^2)/(b^2)=1 m...
Text Solution
|
- Area of the triangle formed by the tangents at the point on the ellips...
Text Solution
|
- If the tangent at any point of the ellipse (x^2)/(a^3)+(y^2)/(b^2)=1 m...
Text Solution
|
- Tangents are drawn to the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 at...
Text Solution
|
- If the tangents drawn from a point on the hyperbola x^(2)-y^(2)=a^(2)-...
Text Solution
|
- From any point on the hyperbola x^(2) -y^(2) =a^(2) -b^(2) two tange...
Text Solution
|
- IF alpha , beta are eccentric angles of end points of a focal cho...
Text Solution
|
- If the tangent at any point of an ellipse x^2/a^2 + y^2/b^2 =1 makes a...
Text Solution
|
- If alpha, beta are the eccentric angles of the extermities of a focal ...
Text Solution
|