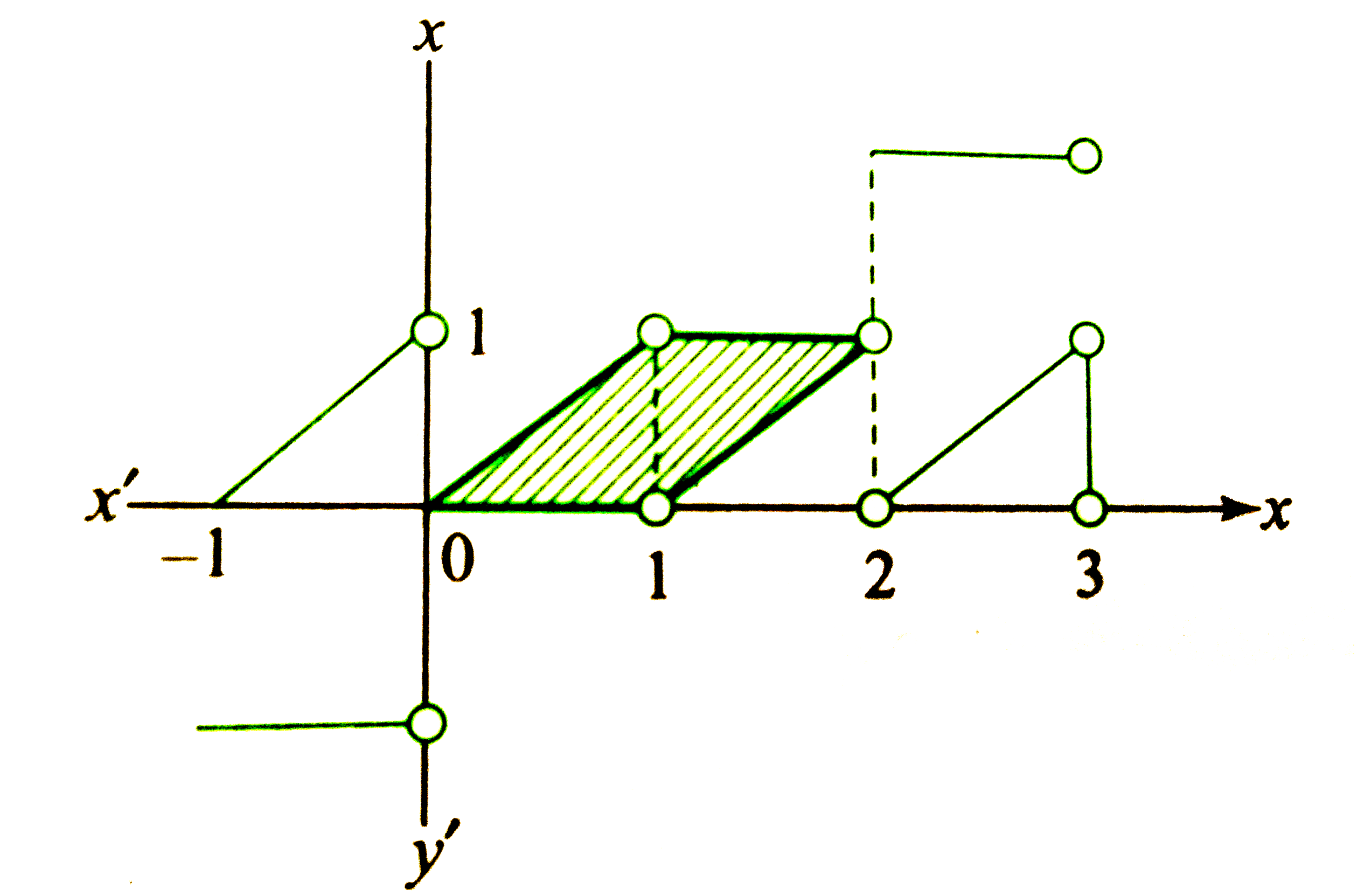
a. `"Area "=2((1)/(2)1xx1)=1` sq. units.
b. `y^(2)=x^(3) and |y|=2x,` both the curve are symmetric about y-axis

`4x^(2)=x^(3)or x=0, 4. `
`"Required area "=2overset(4)underset(0)int(2x-x^(3//2))dx=(32)/(5)` sq. units.
c. `sqrt(x)+sqrt(|y|)=1`
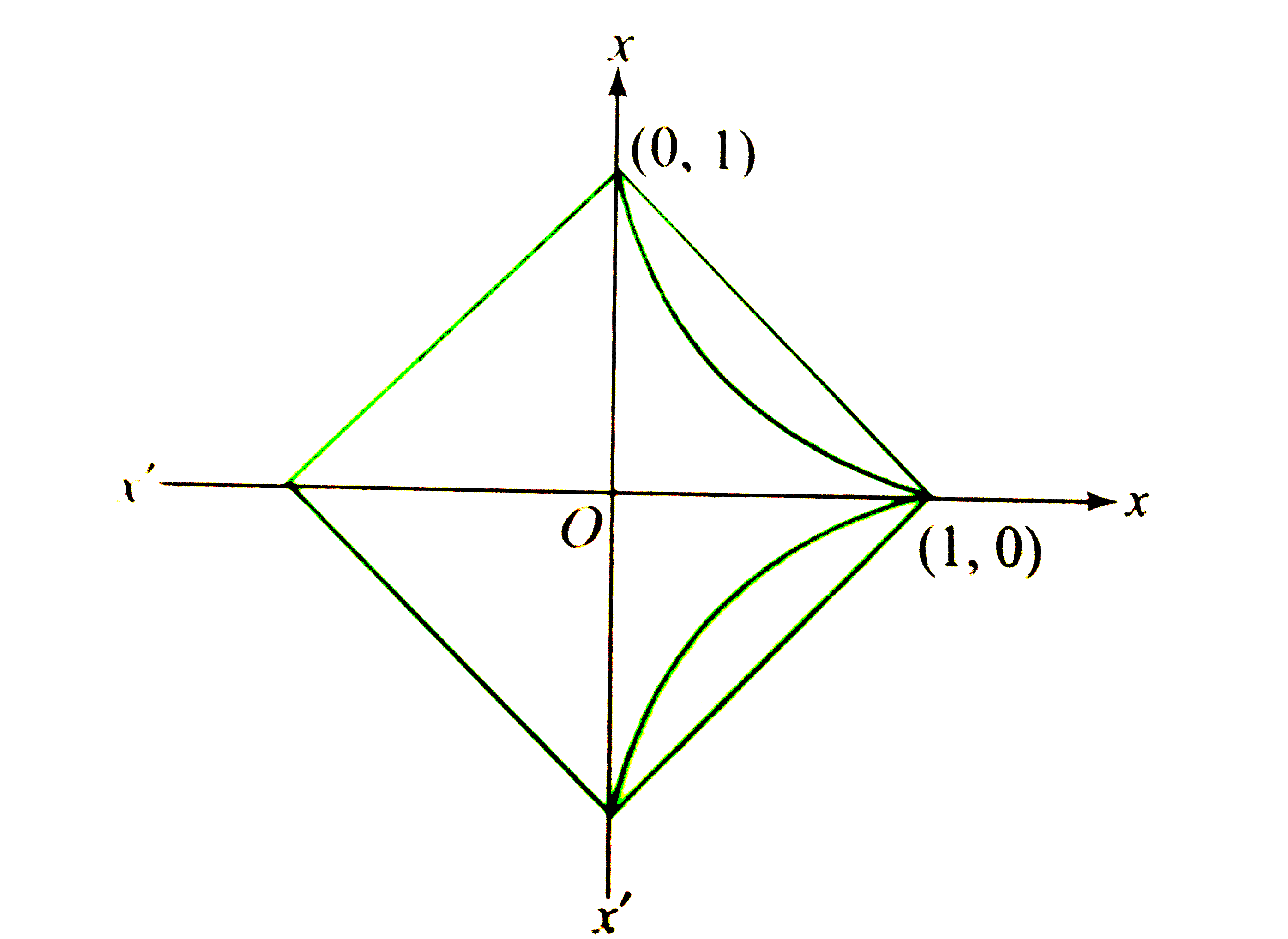
The curve is symmetrical about x-axis
`sqrt(|y|)=1-sqrt(x)and sqrt(x)=1-sqrt(|y|)`
`rArr" for "xgt0,ygt0sqrt(y)=1-sqrt(x)`
`(1)/(2sqrt(y))(dy)/(dx)=-(1)/(2sqrt(x))`
`(dy)/(dx)=-sqrt((y)/(x))`
`(dy)/(dx)lt0," function is decreasing "`
`"Required area "=2overset(1)underset(0)int((1-x)-(1-2sqrt(x)+x))dx`
`=4overset(1)underset(0)int(sqrt(x)-x)dx`
`=4[(x^(3//2))/(3//2)-(x^(2))/(2)]_(0)^(1)`
`=4[(2)/(3)-(1)/(2)]`
`=(2)/(3)` sq. units.
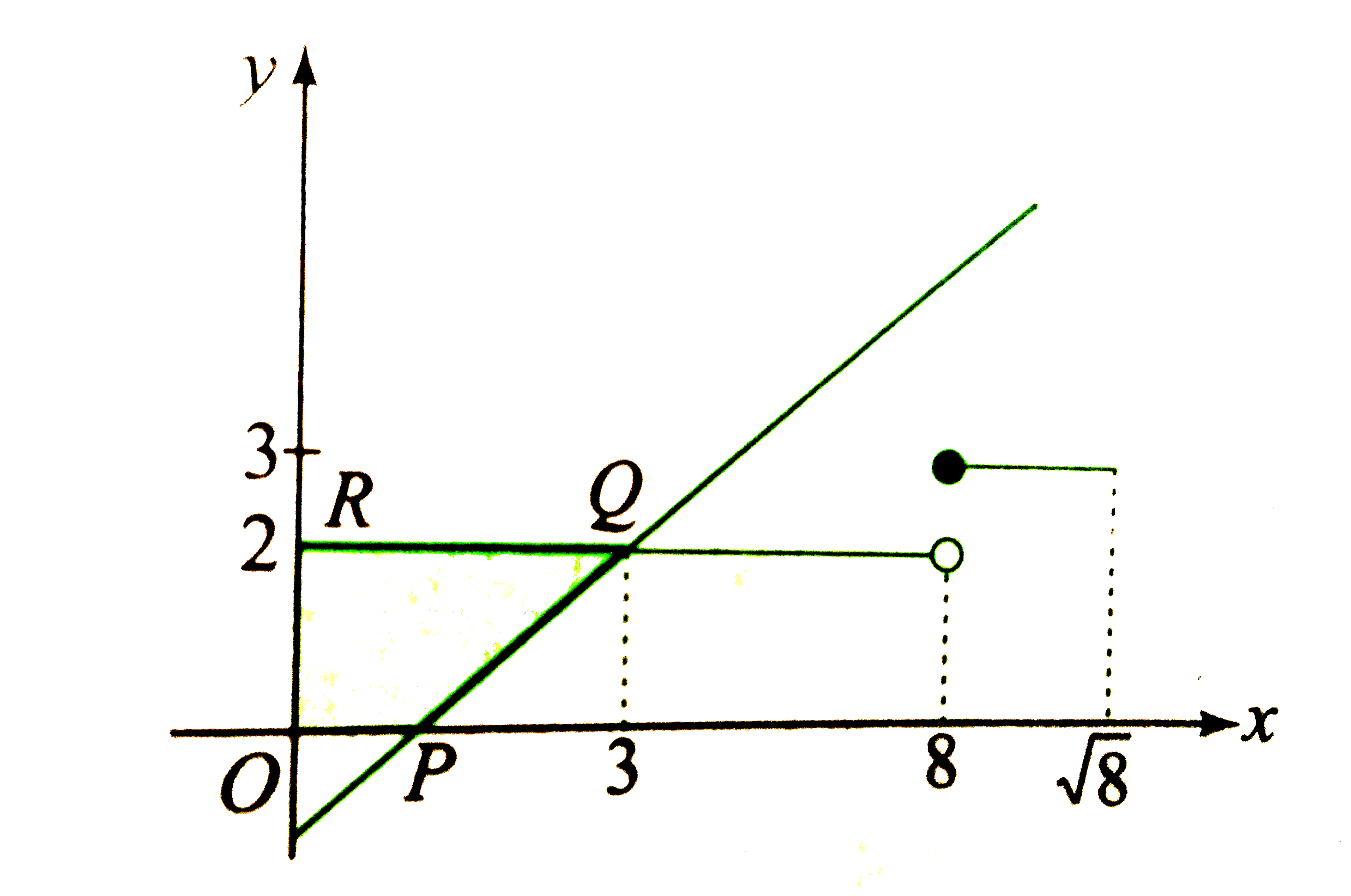
d. If `-8ltxlt8,` then y=2.
`"If "x in (-8sqrt(2),-8]cup[8,8sqrt(2))," then "y=3,` and so on
Intersection of `y=x-1 and y=2." We get "x=3 in (-8,8).`
Intersection of `y=x-1 and y=3`.
`"We get "x=4 notin (-8sqrt(2),-8]cup[8,8sqrt(2))`.
`"Similarly, "y = x-1" will not intersect "y=[(x^(2))/(64)+2]" at any"`
other integral, except in the interval `x in (-8,8).`
Required area (shaded region ) `=2xx3-(1)/(2)xx2xx2`
=4 sq. units.