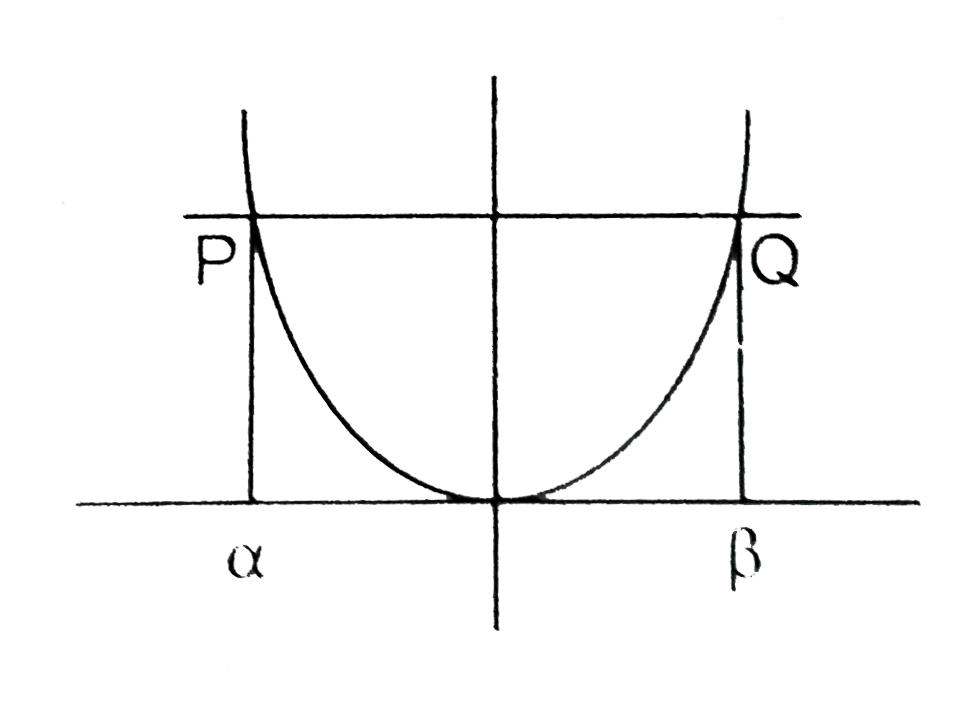
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A variable line L intersects the parabola y=x^(2) at points P and Q wh...
Text Solution
|
- A variable chord PQ of the parabola y^(2)=4x is down parallel to the l...
Text Solution
|
- If cos(alpha-beta) and cos(alpha+beta) are the length of segments of a...
Text Solution
|
- P and Q are any two points on the circle x^(2)+y^(2)=4 such that PQ is...
Text Solution
|
- IF (alpha, beta) is a point on the chord PQ of the circle x^(2)+y^(2)=...
Text Solution
|
- बिंदु P (-4 ,2 ) को निरूपित कर बिंदु Q के निर्देशांक ज्ञात कीजिए यदि र...
Text Solution
|
- The straight lines y=+-x intersect the parabola y^(2)=8x in points P a...
Text Solution
|
- A variable chord PQ of the parabola y^(2) = 4x is drawn parallel to th...
Text Solution
|
- A variable tangent to the parabola y^(2)=4ax meets the parabola y^(2) ...
Text Solution
|