Home
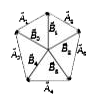
Class 11
PHYSICS
The five sides of a regular pentagon are...

The five sides of a regular pentagon are represented by vectors `vec(A)_(1), vec(A)_(2), vec(A)_(3), vec(A)_(4)` and `vec(A)_(5)` in cyclic order as shown. Corresponding vertices are represented by `vec(B)_(1), vec(B)_(2), vec(B)_(3), vec(B)_(4) and vec(B)_(5)` drawn from the centre of the pentagon. Then, `vec(B)_(2) + vec(B)_(3) + vec(B)_(4) + vec(B)_(5)`=

A

`vec(A)_(1)`

B

`- vec(A)_(1)`

C

`vec(B)_(1)`

D

`- vec(B)_(1)`

Text Solution

Verified by Experts

The correct Answer is:
D
Since, `vec(B)_(1) + vec(B)_(2) + vec(B)_(3) + vec(B)_(4) + vec(B)_(5)= 0`
This is because of regular pentagon Hence, `vec(B)_(2) + vec(B)_(3) + vec(B)_(4) + vec(B)_(5)= - vec(B)_(1)`
Promotional Banner

Similar Questions

Explore conceptually related problems

If |vec(a)|=3, |vec(b)|=4 and |vec(a)-vec(b)|=5 , then what is the value of |vec(a)+vec(b)|=?

If |vec(a) | = 3, |vec(b)|= 4 and |vec(a)- vec(b)|=5 , then what si the value of |vec(a) + vec(b)| =?

Given that vec(A)+vec(B)=vec(C ) . If |vec(A)|=4, |vec(B)|=5 and |vec(C )|=sqrt(61) , the angle between vec(A) and vec(B) is

vec(a)+vec(b)+vec(c)=vec(0) such that |vec(a)|=3, |vec(b)|=5 and |vec(c)|=7 . What is vec (a). vec(b) + vec(b). vec(c) + vec(c). vec (a) equal to ?

Show that the points whose position vectors are vec(a) + 2vec(b) + 5vec(c), 3vec(a) + 2vec(b) + vec(c), 2vec(a) + 2vec(b) + 3vec(c) are colliner.

If vec(a) and vec(b) are vectors such that |vec(a)|=sqrt(3), |vec(b)|=2 and vec(a).vec(b)=sqrt(6) then the angle between vec(a) and vec(b) is

If vec(a)+vec(b)+vec(c )=0 " and" |vec(a)|=3,|vec(b)|=5, |vec(c )|=7 , then find the value of vec(a),vec(b)+vec(b).vec(c )+vec(c ).vec(a) .

If vec(A)=vec(B)+vec(C ) , and the magnitudes of vec(A) , vec(B) , vec(C ) are 5,4, and 3 units, then the angle between vec(A) and vec(C ) is

If vec(a) and vec(b) are mutually perpendicular unit vectors then (3vec(a)+2vec(b)).(5vec(a)-6vec(b))=?