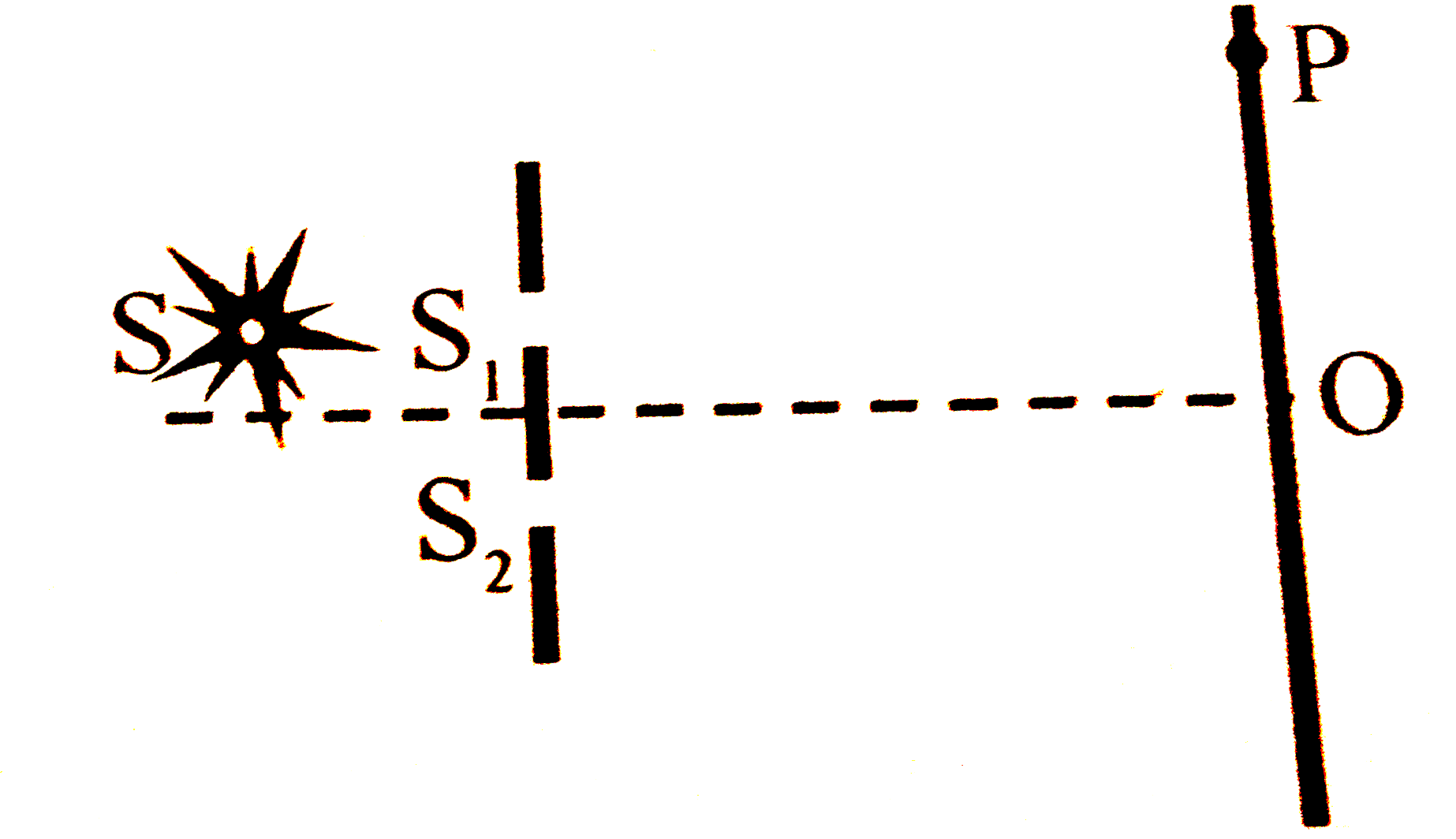Text Solution
Verified by Experts
|
Topper's Solved these Questions
TEST PAPER
ALLEN|Exercise PHYSICS|4 VideosView PlaylistTEST PAPER 2
ALLEN|Exercise PHYSICS|45 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
ALLEN-TEST PAPER 1-PHYSICS
- Why are electric field lines perpendicular at a point on an equipotent...
02:06
|
Play - When unpolarised light is incident on the interface separating the rar...
01:39
|
Play - For the same angle of incidence, the angles of refraction in three dif...
03:31
|
Play - Write the necessary conditions for the phenomenon of total internal re...
02:45
|
Play - Answer the following, giving reason:- (a) When light travels from ...
03:07
|
Play - An object is immersed in some liquid. Prove that .(a)n(l)=("Real d...
08:15
|
Play - Five point charges, each +q are placed on five vertices of a regular h...
04:06
|
Play - The figure shows a modified Young’s double slit experimental set-up. H...
06:11
|
Playing Now - A small ink dot on a paper is viewed through a glass slab of thickness...
03:03
|
Play - Using Gauss’ law, derive an expression for the electric field at a poi...
05:01
|
Play - (a) Derive the relation a sin theta=lambda for the first minimum of t...
13:27
|
Play