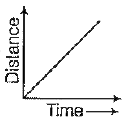
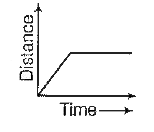
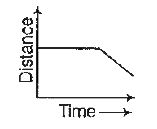
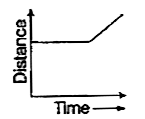
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
KINEMATICS
DC PANDEY|Exercise Subjective|51 VideosView PlaylistKINEMATICS
DC PANDEY|Exercise More Than One Correct|6 VideosView PlaylistKINEMATICS
DC PANDEY|Exercise Assertion And Reason|12 VideosView PlaylistGRAVITATION
DC PANDEY|Exercise (C) Chapter Exercises|45 VideosView PlaylistKINEMATICS 1
DC PANDEY|Exercise INTEGER_TYPE|15 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
DC PANDEY-KINEMATICS-Objective
- The horizontal and vertical displacements of a particle moving along a...
03:43
|
Play - A ball is released from the top of a tower of height h metre. It takes...
04:01
|
Play - An ant is at a corner of a cubical room of side a. The ant can move wi...
10:58
|
Playing Now - A lift starts from rest. Its acceleration is plotted against time. Whe...
06:29
|
Play - A lift performs the first part of its ascent with uniform acceleration...
08:20
|
Play - Two objects are moving along the same straight line. They cross a poin...
05:42
|
Play - A cart is moving horizontally along a straight line with constant spee...
04:34
|
Play - The figure shows velocity-time graph of a particle moving along a stra...
05:05
|
Play - A ball is thrown vertically upwards from the ground and a student gazi...
02:27
|
Play - A body starts moving with a velocity v0 = 10 ms^-1. It experiences a r...
02:43
|
Play - Two trains are moving with velocities v1 = 10 ms^-1 and v2 = 20 ms^-1 ...
04:20
|
Play - Two balls of equal masses are thrown upwards, along the same vertical ...
03:30
|
Play - A particle is projected vertically upwards and reaches the maximum hei...
02:55
|
Play - A particle moves along the curve y = x^2 /2. Here x varies with time a...
03:47
|
Play - If the displacement of a particle varies with time as sqrt x = t+ 3
01:50
|
Play - The graph describes an airplane's acceleration during its take-off run...
03:38
|
Play - A particle moving in a straight line has velocity-displacement equatio...
02:55
|
Play - A particle is thrown upwards from ground. It experiences a constant re...
07:59
|
Play - A body of mass 10 kg is being acted upon by a force 3t^2 and an opposi...
04:26
|
Play - A stone is thrown vertically upwards. When stone is at a height half o...
03:02
|
Play