A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
KINEMATICS
DC PANDEY|Exercise More Than One Correct|6 VideosView PlaylistKINEMATICS
DC PANDEY|Exercise Comprehension|7 VideosView PlaylistKINEMATICS
DC PANDEY|Exercise Objective|45 VideosView PlaylistGRAVITATION
DC PANDEY|Exercise (C) Chapter Exercises|45 VideosView PlaylistKINEMATICS 1
DC PANDEY|Exercise INTEGER_TYPE|15 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
DC PANDEY-KINEMATICS-Subjective
- A train stopping at two stations 4 km apart takes 4 min on the journey...
05:40
|
Play - When a man moves down the inclined plane with a constant speed 5 ms^-1...
07:36
|
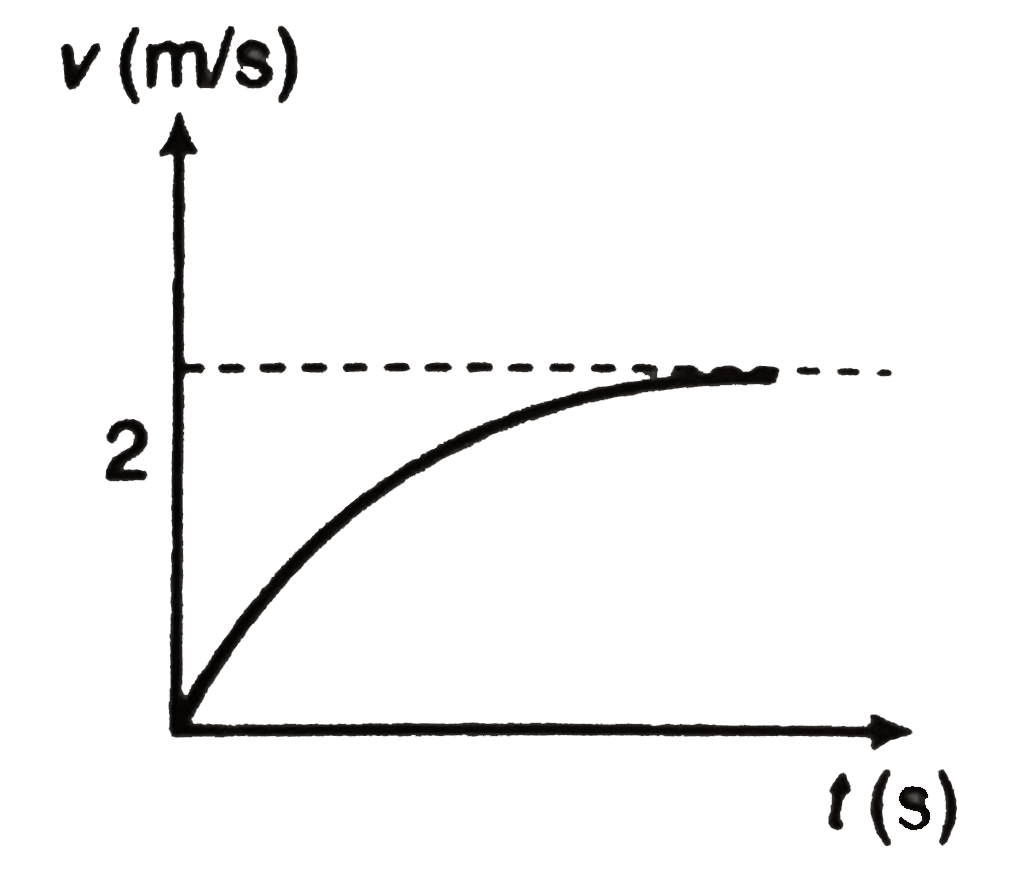
Play - Equation of motion of a body is (dv)/(dt) = -4v + 8, where v is the ve...
09:38
|
Playing Now - Two particles A and B are placed in gravity free space at (0, 0, 0) m ...
04:03
|
Play - Velocity of the river with respect to ground is given by v0. Width of ...
03:20
|
Play - The relation between time t and displacement x is t = alpha x^2 + beta...
03:30
|
Play - A street car moves rectilinearly from station A to the next station B ...
05:02
|
Play - A particle of mass m moves on positive x-axis under the influence of f...
03:48
|
Play - A partial along a straight line whose velocity-displacement graph is a...
02:07
|
Play - A particle is falling freely under gravity. In first t second it cover...
03:12
|
Play - A rod AB is shown in figure. End A of the rod is fixed on the ground. ...
04:49
|
Play - A thief in a stolen car passes through a police check post at his top ...
07:30
|
Play - Anoop (A) hits a ball along the ground with a speed u in a direction w...
03:31
|
Play - A car is travelling on a straight road. The maximum velocity the car C...
08:05
|
Play - A car is travelling on a road. The maximum velocity the car can attain...
05:02
|
Play - Two particles are moving along two long straight lines, in the same pl...
10:48
|
Play - A particle having a velocity v = v0 at t= 0 is decelerated at the rate...
04:35
|
Play - At time t = 0, a car moving along a straight line has a velocity of 16...
09:13
|
Play - An object moves with constant acceleration a. Which of the following e...
01:01
|
Play - Ship A is located 4 km north and 3 km east of ship B. Ship A has a vel...
04:13
|
Play