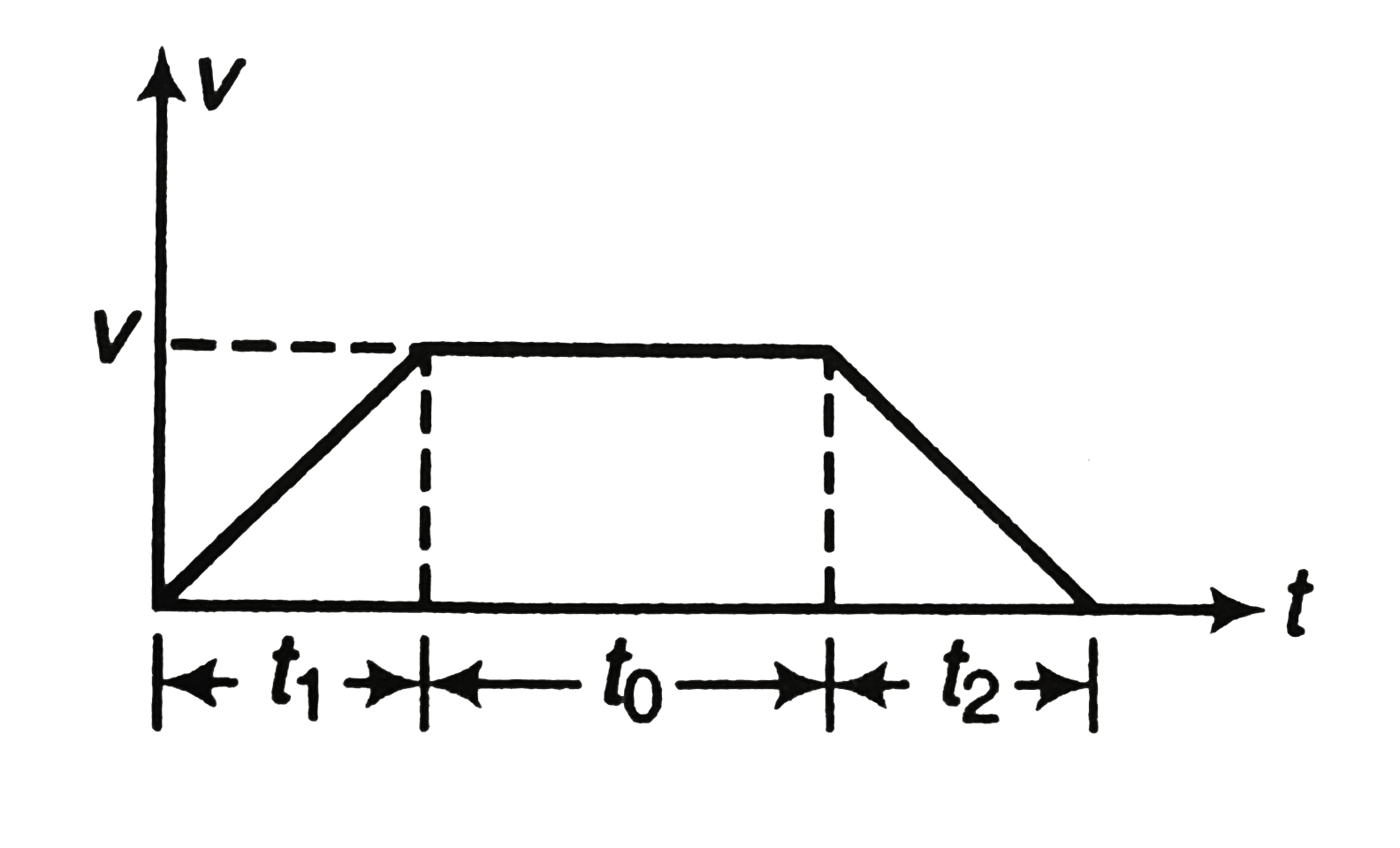
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
KINEMATICS
DC PANDEY|Exercise Comprehension|7 VideosView PlaylistKINEMATICS
DC PANDEY|Exercise Subjective Questions|24 VideosView PlaylistKINEMATICS
DC PANDEY|Exercise Subjective|51 VideosView PlaylistGRAVITATION
DC PANDEY|Exercise (C) Chapter Exercises|45 VideosView PlaylistKINEMATICS 1
DC PANDEY|Exercise INTEGER_TYPE|15 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
DC PANDEY-KINEMATICS-More Than One Correct
- Identify the correct graph represeriting the motion of a particle alon...
01:56
|
Play - A man who can swim at a velocity v relative to water wants to cross a ...
04:24
|
Play - The figure shows the velocity (v) of a particle plotted against time (...
03:44
|
Play - The speed of a train increases at a constant rate alpha from zero to v...
09:09
|
Playing Now - A particle moves in x-y plane and at time t is at the point (t^2, t^3 ...
03:03
|
Play - A car is moving with uniform acceleration along a straight line betwee...
10:09
|
Play