A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
WORK, ENERGY & POWER
DC PANDEY|Exercise Exercise 9.1|10 VideosView PlaylistWORK, ENERGY & POWER
DC PANDEY|Exercise Exercise 9.2|9 VideosView PlaylistWORK, ENERGY & POWER
DC PANDEY|Exercise TYPE2|1 VideosView PlaylistWAVE MOTION
DC PANDEY|Exercise Integer Type Question|11 VideosView PlaylistWORK, ENERGY AND POWER
DC PANDEY|Exercise MEDICAL ENTRACES GALLERY|33 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
DC PANDEY-WORK, ENERGY & POWER-Miscellaneous Example
- A small mass m starts from rest and slides down the smooth spherical s...
03:28
|
Playing Now - A smooth track in the form of a quarter-circle of radius 6 m lies in t...
08:34
|
Play - A single conservative force F(x) acts on a on a (1.0kg ) particle that...
07:42
|
Play - A small disc A slides down with initial velocity equal to zero from th...
06:55
|
Play - A small disc of mass m slides down a smooth hill of height h without i...
10:04
|
Play - Two blocksA andB are connected to each other by a string and a spring ...
03:15
|
Play
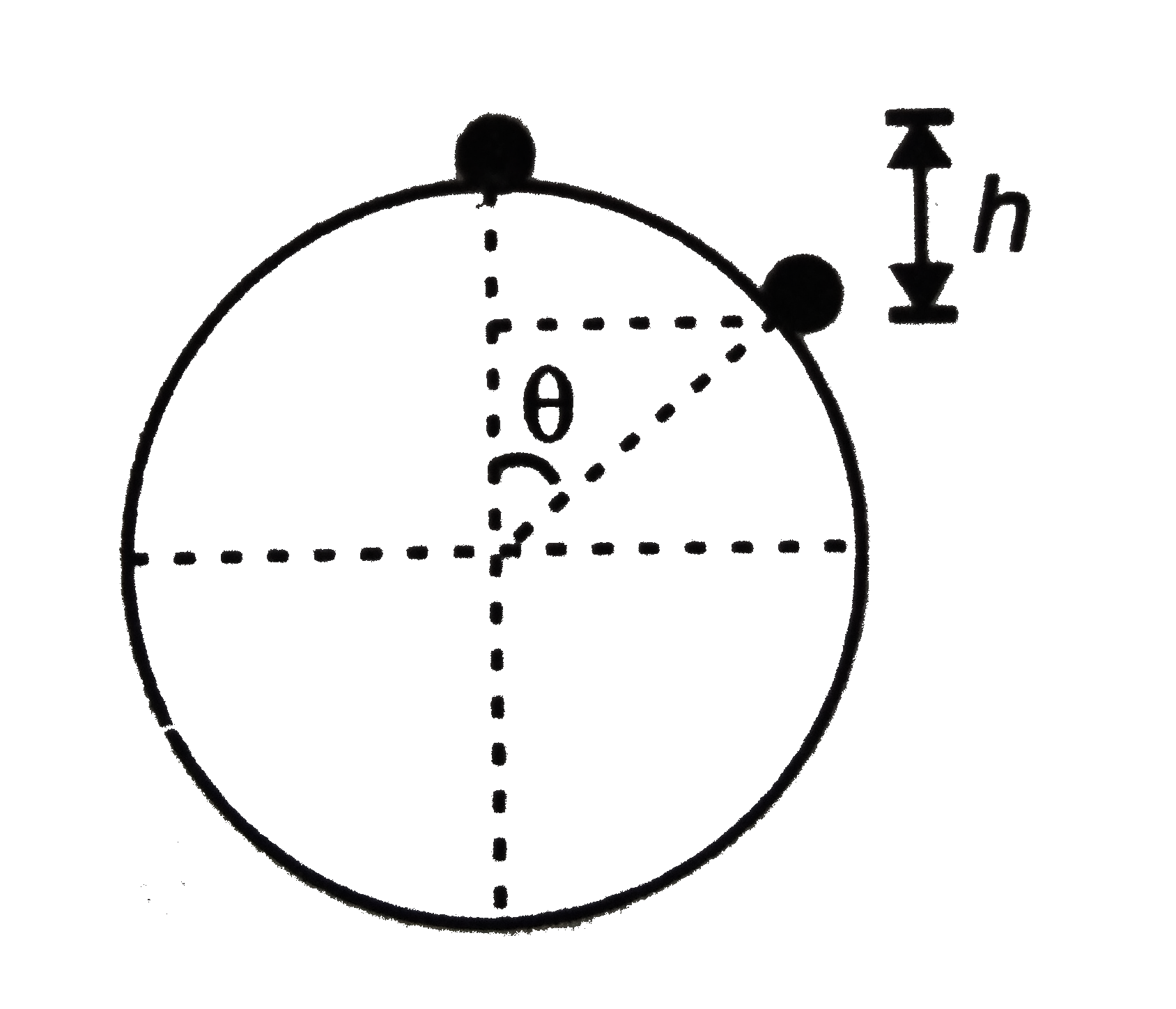 .
.