A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
CIRCULAR MOTION
DC PANDEY|Exercise Level 1 Subjective|13 VideosView PlaylistCIRCULAR MOTION
DC PANDEY|Exercise Level 2 Single Correct|18 VideosView PlaylistCIRCULAR MOTION
DC PANDEY|Exercise Assertion And Reason|28 VideosView PlaylistCENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
DC PANDEY|Exercise Level 2 Subjective|21 VideosView PlaylistCOMMUNICATION SYSTEM
DC PANDEY|Exercise Only One Option is Correct|27 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
DC PANDEY-CIRCULAR MOTION-Level 1 Objective
- A particle is revolving in a circle with increasing its speed uniforml...
01:55
|
Play - A particle is moving in a circular path with a constant speed. If thet...
02:01
|
Play - A simple pendulum of length l has maximum angular displacement theta ....
02:26
|
Play - A particle of mass m is fixed to one end of a light rigid rod of lengt...
00:58
|
Play - A simple pendulum of length l and mass m is initially at its lowest po...
01:46
|
Play - A point moves along a circle having a radius 20cm with a constant tang...
01:35
|
Play - A ring of mass 2pikg and of radius 0.25m is making 300rp m about an ax...
04:45
|
Play - A car is moving on a circular level road of curvature 300m . If the co...
03:12
|
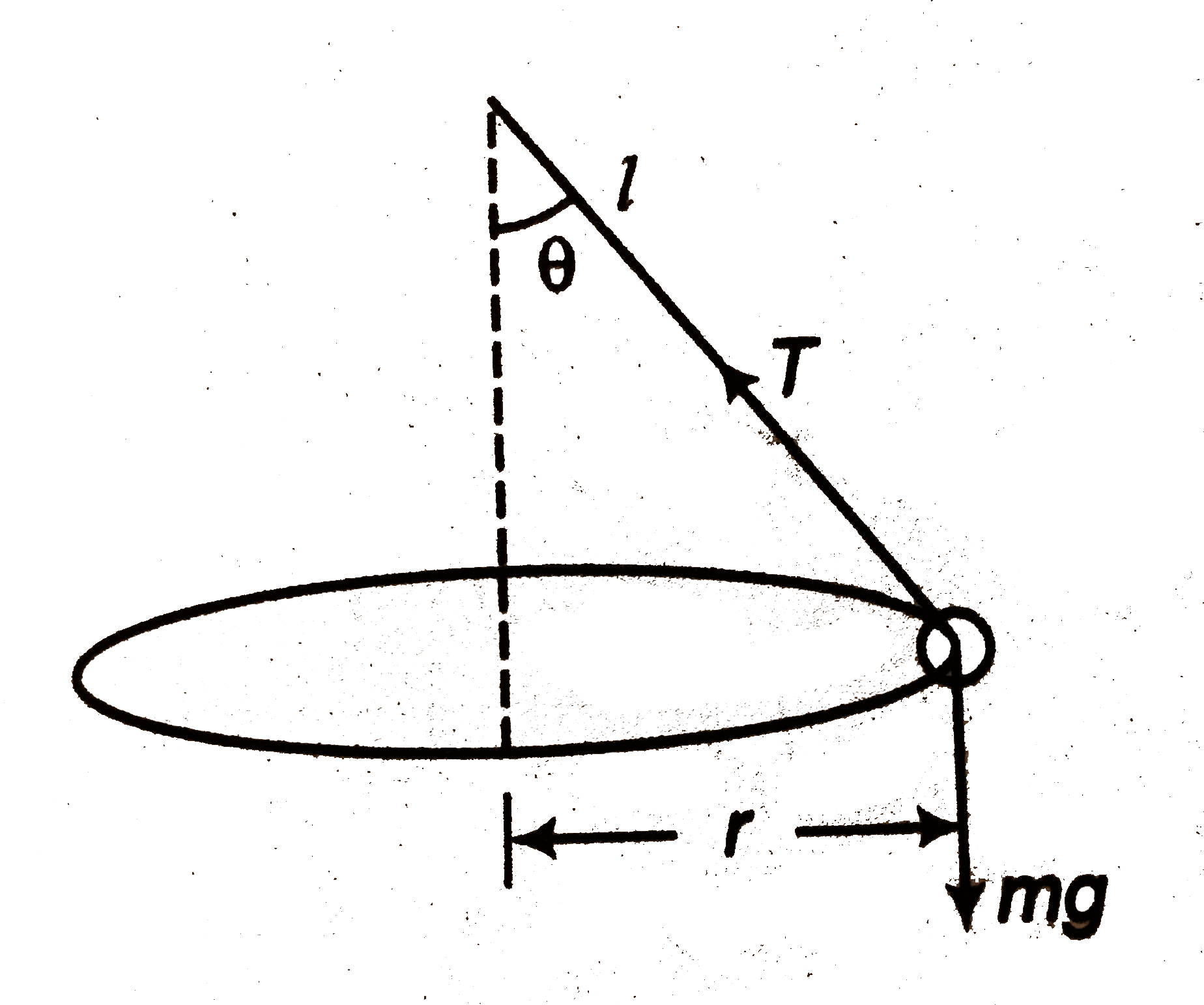
Play - In a conical pendulum arrangement, a string of length 1 m is fixed at ...
03:58
|
Playing Now - In the previous question, the tension in the string is
04:10
|
Play - A small particle of mass 036g rests on a horizontal turntable at a dis...
03:04
|
Play - A simple pendulum of length l and bob of mass m is displaced from its ...
03:19
|
Play - Two particles revolve concentrically in a horizontal plane in the same...
02:14
|
Play - Three particles A,B and C move in a circle in anticlockwise direction...
04:12
|
Play