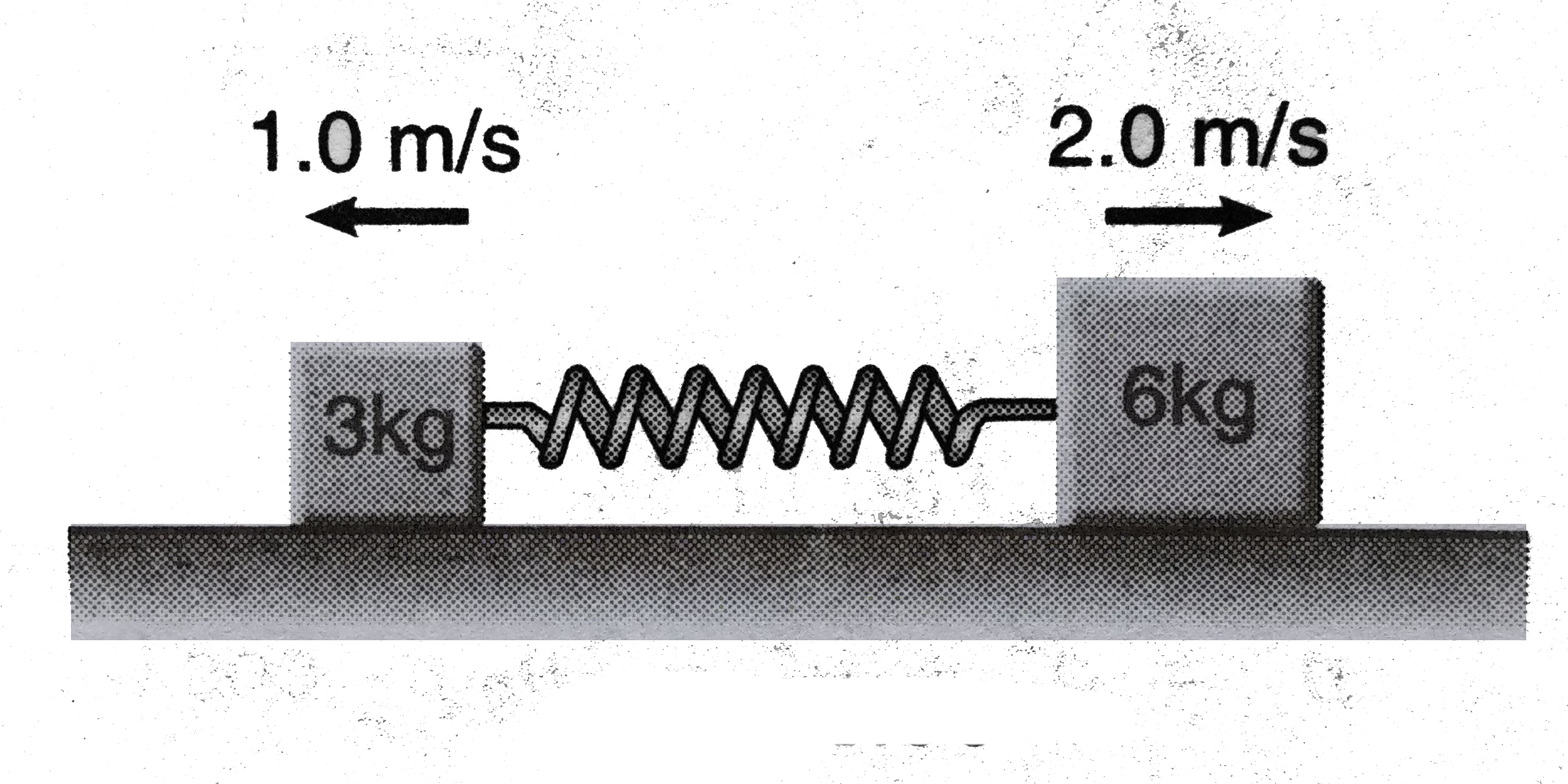Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
DC PANDEY|Exercise Level 1 Assertion and Reason|15 VideosView PlaylistCENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
DC PANDEY|Exercise Level 1 Objective|42 VideosView PlaylistCENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
DC PANDEY|Exercise Exercise 11.5|4 VideosView PlaylistCENTRE OF MASS, IMPULSE AND MOMENTUM
DC PANDEY|Exercise Comprehension type questions|15 VideosView PlaylistCIRCULAR MOTION
DC PANDEY|Exercise Medical entrances s gallery|19 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
DC PANDEY-CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION-Exercise 11.6
- Two blocks of masses 3kg and 6kg respectivley are placed on a smooth h...
06:38
|
Playing Now - A moving body of mass m makes a head on elastic collision with another...
05:42
|
Play - What is the fractional decrease in kinetic energy of a body of mass m1...
09:12
|
Play - In one dimensional elastic collison of equla masses, the velocities ar...
03:03
|
Play - After an head on elastic collision between two balls of equal masses, ...
05:45
|
Play - A ball of mass 1kg moving with 4m^-1 along +x-axis collides elasticall...
05:18
|
Play - Three balls A, B and C are placed on a smooth horizontal surface. Give...
09:54
|
Play - Ball 1 collides directly with another identical ball 2 at rest. Veloci...
04:09
|
Play - A sphere A of mass m, travelling with speed v, collides directly with ...
03:07
|
Play - A smooth sphere is moving on a horizontal surface with velocity vector...
04:56
|
Play - A ball falls vertically on an inclined plane of inclination alpha with...
01:42
|
Play