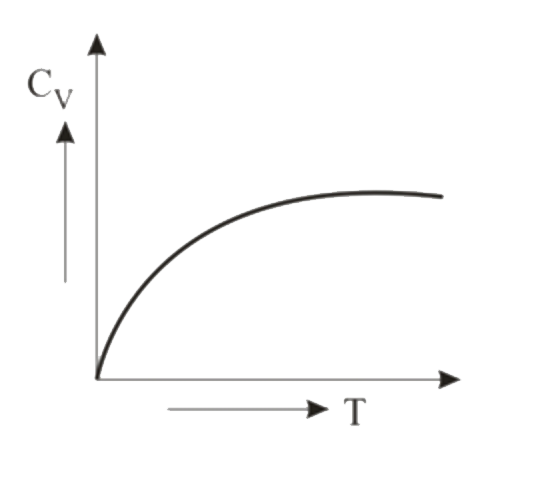
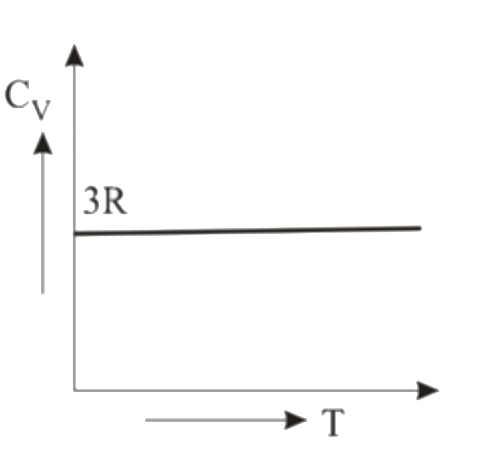
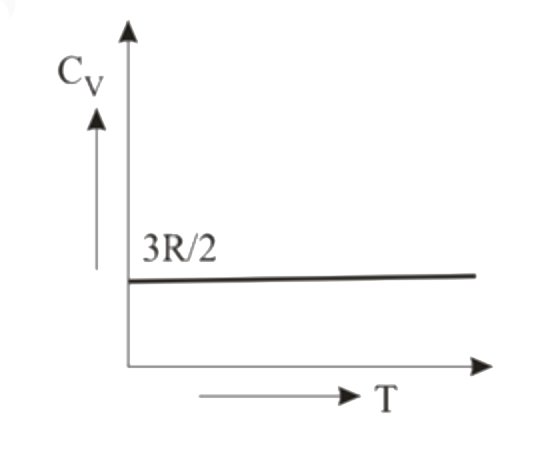
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
LAWS OF THERMODYNAMICS
DC PANDEY|Exercise Exercise 21.1|1 VideosView PlaylistLAWS OF THERMODYNAMICS
DC PANDEY|Exercise Exercise 21.2|7 VideosView PlaylistLAWS OF THERMODYNAMICS
DC PANDEY|Exercise Example Type 3|1 VideosView PlaylistLAWS OF MOTION
DC PANDEY|Exercise Medical entrances gallery|39 VideosView PlaylistMAGNETIC EFFECT OF CURRENT AND MAGNETISM
DC PANDEY|Exercise Integer type Questions|10 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
DC PANDEY-LAWS OF THERMODYNAMICS-Miscellaneous Example
- For a Carnot cycle (or engine) discussed in article 21.4, prove that e...
20:53
|
Play - Find the molar specific heat of the process p=a/T for a monoatomic gas...
03:43
|
Playing Now - At 27^@C two moles of an ideal monatomic gas occupy a volume V. The ga...
04:09
|
Play - Two moles of a diatomic ideal gas is taken through pT= constant. Its t...
02:42
|
Play - An ideal monoatomic gas at temperature 27^@C and pressure 10^6N//m^2 o...
04:55
|
Play - One mole of a monoatomic ideal gas is taken through the cycle shown in...
09:54
|
Play - A gas undergoes a process such that pprop1/T. If the molar heat capaci...
04:29
|
Play - A gaseous mixture enclosed in a vessel consists of one gram mole of a ...
04:40
|
Play - An ideal gas having initial pressure p, volume V and temperature T is ...
06:34
|
Play