Home
Class 12
PHYSICS
The electric field in a region is given ...

The electric field in a region is given by `E=alphaxhati`. Here `alpha` is a constant of proper dimensions. Find
a. the total flux passing throug a cube bounded by the surface `x=l, x=2l, y=0, y=l, z=0, z=l`.
b. the charge contained inside in above cube.

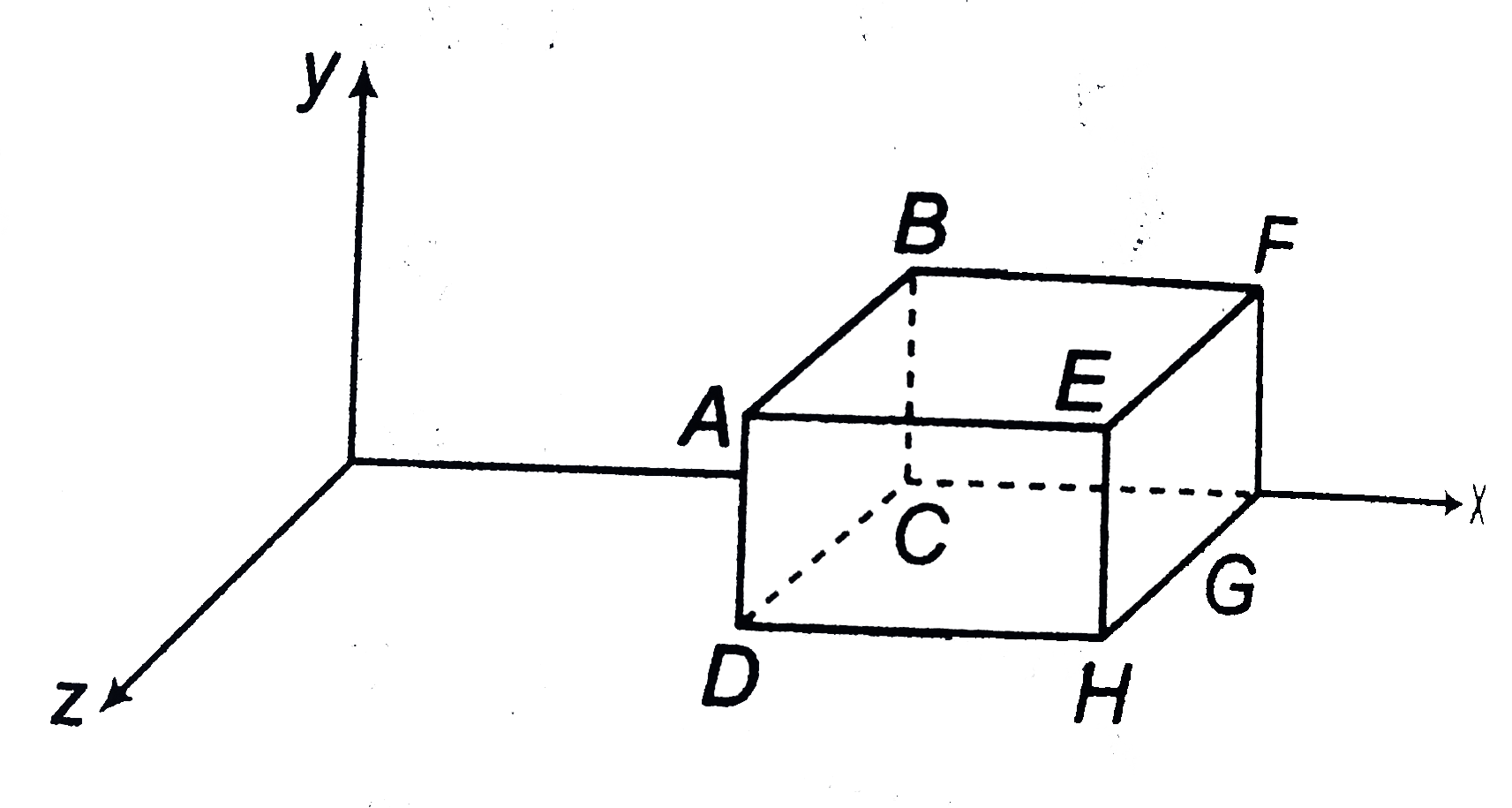
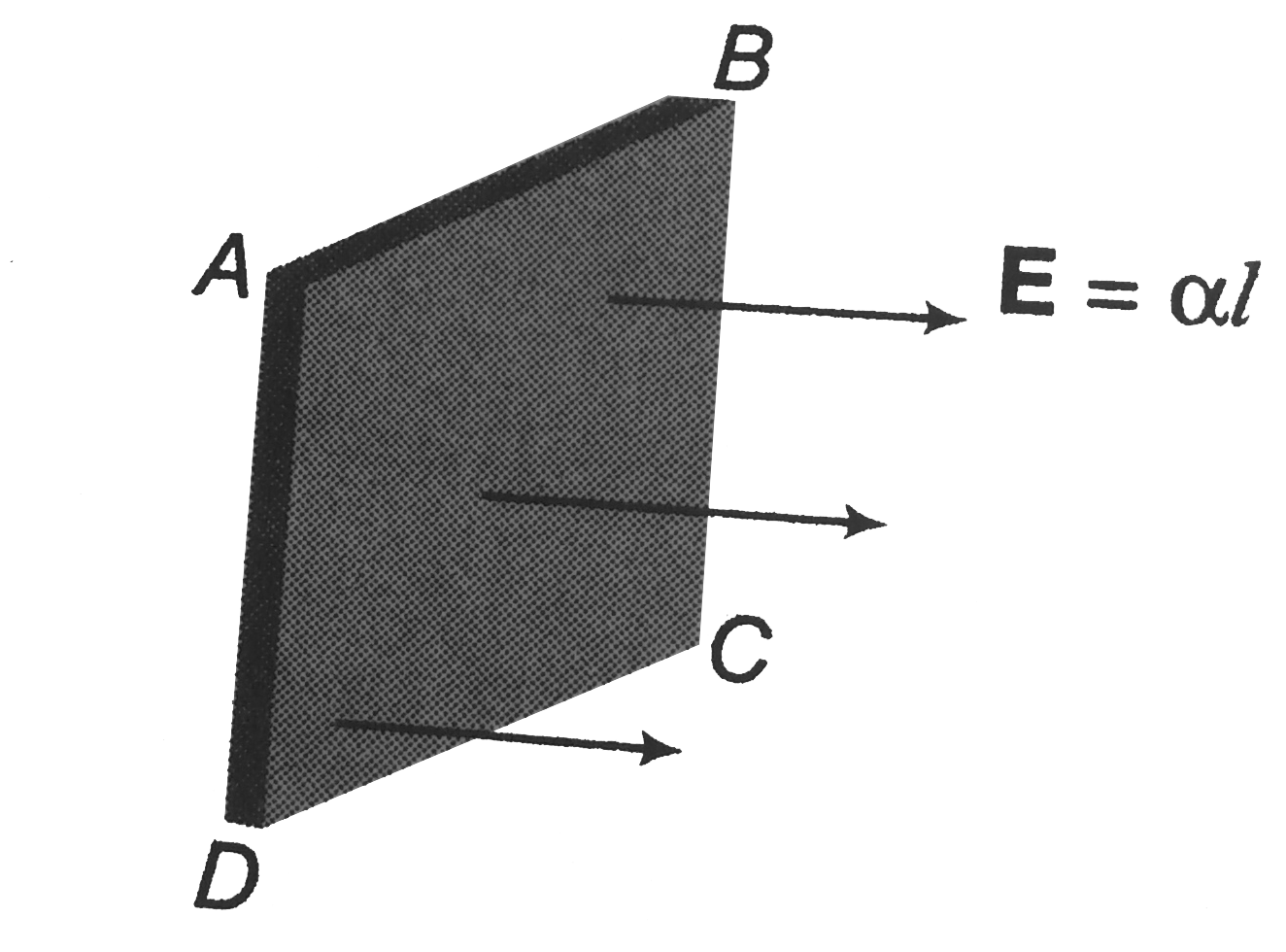
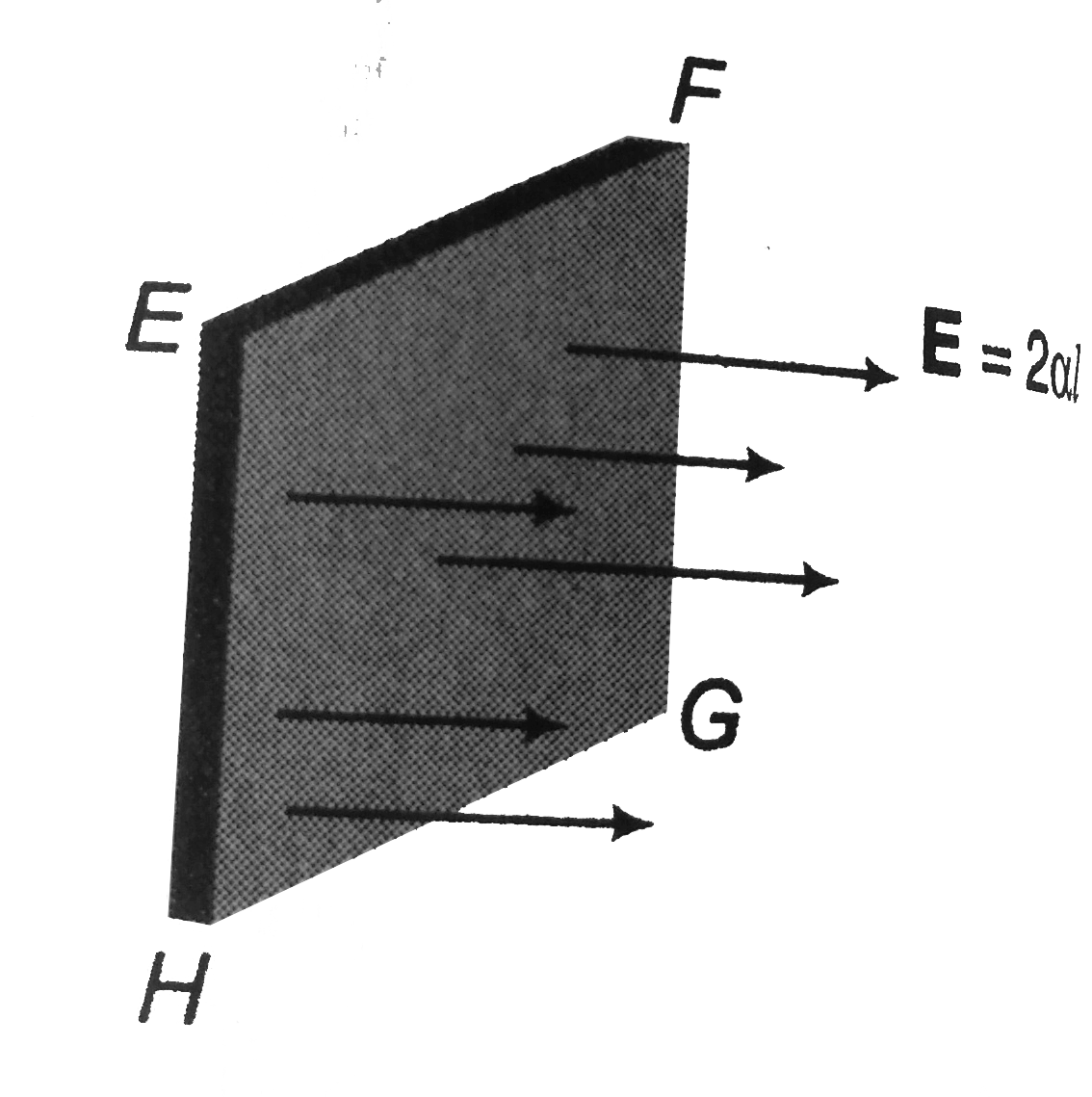
Text Solution

Verified by Experts

The correct Answer is:
A, B, C
a. Electric field is along positive x x-direction. Therfore,field lines are perpendicular to face `ABCD` and `EFGH`. At all other four faces field lines are tangential. So, net flux passing through these four facess will be zero.
Flux entering at face `ABCD` at this face `x=l`
`:. E=alpha lhati`
`:.` Flux entering the cube from this face
`phi_1=ES=(alphal)(l^2)=alphal^3`
Flux leaving the face `EFGH` At this face `x=2l`
`:. E=2alphalhati`
`:.` Flux coming out of this face
`phi_2=ES=(2alphal)(l^2)`
`=2alphal^3`
`:.` Net flux passing through the cube,
`phi_("net")=phi_2-phi_1=2alphal^3-alphal^3`
`=alphal^3`
b. From Gauss's law,
`phi_("net")=(q_"in")/epsilon_0`
`q_("in")=(phi_("net")(epsilon_0)`
`=alpha epsilon l^3`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • ELECTROSTATICS

    DC PANDEY|Exercise Exercise 24.1|4 Videos

  • ELECTROSTATICS

    DC PANDEY|Exercise Exercise 24.2|9 Videos

  • ELECTROSTATICS

    DC PANDEY|Exercise Example Type 8|3 Videos

  • ELECTROSTATIC POTENTIAL AND CAPACITORS

    DC PANDEY|Exercise (C) Chapter exercises|50 Videos

  • GRAVITATION

    DC PANDEY|Exercise All Questions|120 Videos

Similar Questions

Explore conceptually related problems

The electric field in a region is given by vec (E ) = (E_(0))/(a) x hat(i) . Find the electric flux passing through a cubical volume bounded by the surfaces x = 0 , x = a , y = 0 , y = a , z = 0 and z = a .

The electric field in a region is given by E = (E_0x)/lhati . Find the charge contained inside a cubical 1 volume bounded by the surfaces x=0, x=a, y=0, yh=, z=0 and z=a. Take E_0=5xx10^3N//C l=2cm and a=1m.

Knowledge Check

  • The electric field in a region is given by E = 3/5 E_0hati +4/5E_0j with E_0 = 2.0 x 10^3 N//C . Find the flux of this field through a rectangular surface of area 0.2 m^2 parallel to the y-z plane.

    A
    `24Nm^2//C`
    B
    `240Nm^2//C`
    C
    `440Nm^2//C`
    D
    `44Nm^2//C`

  • Due to a charge inside the cube, the electric field is: E_(x) = 600x, E_(y) = 0, E_(z) = 0. The charge inside the cube is nearly -

    A
    600`mu`C
    B
    60`mu`C
    C
    53`mu`C
    D
    6`mu`C

  • An infinite wire having charge density lambda passes through one of the edges of a cube having length l. find the total flux passing through the cube

    A
    `(lambdal)/(epsilon_(0))`
    B
    `(lambdal)/(4epsilon_(0))`
    C
    `(lambdal)/(6epsilon_(0))`
    D
    None of these

    • Similar Questions

    Explore conceptually related problems

    The electric field in a region is given by vec(E)=E_(0)x hat(i) . The charge contained inside a cubical volume bounded by the surface x=0, x=2m, y=0, y=2m, z=0 and z=2m is n epsi_(0)E_(0) . Find the va,ue of n.

    The electric field I a region is given gy vecE=(E_(0)x)/(b)hati . Find the charge contained in the ubical volume bounded by the surfaces x=0, x=a, y=0, y=0,z=0 and z=a. take E_(0)=5xx10^(3)NC^(-1),a=1cm and b=2cm .

    The electric field in a region is given by vecE=E_0x/iota veci . Find the charge contained inside a cubical volume bounded by the curfaced x=0, x=alpha, y=0, y=alpha, z=0 and z= alpha . Take E_0= 5 xx 10^3 N C^(-1) , iota= 2cm and alpha=1 cm .

    The electric fields in a region is given by vec(E)=E_(0)(x)/(L)hat(i) ,Find the charge contained inside a cubical volume bounded by the surface x=0,x=L,y=0,y=L,z=0,z=L .

    Five electric dipoles having charges +q and -q are placed inside a cube having each side of length l . The total electric flux coming out of the cube is given by

    Home
    Profile