Let us find the magnetic field at point P inside the cavity at a distace `r_1` and ) and `r_2` from C.
`J="current per unit area"`
`R="radius of cylinder"`
`a="radius of cavity"`
`i_1` whole current from cylinder `=J(pir^2)`
`i_2=` curent from hole `=J(pia^2)`
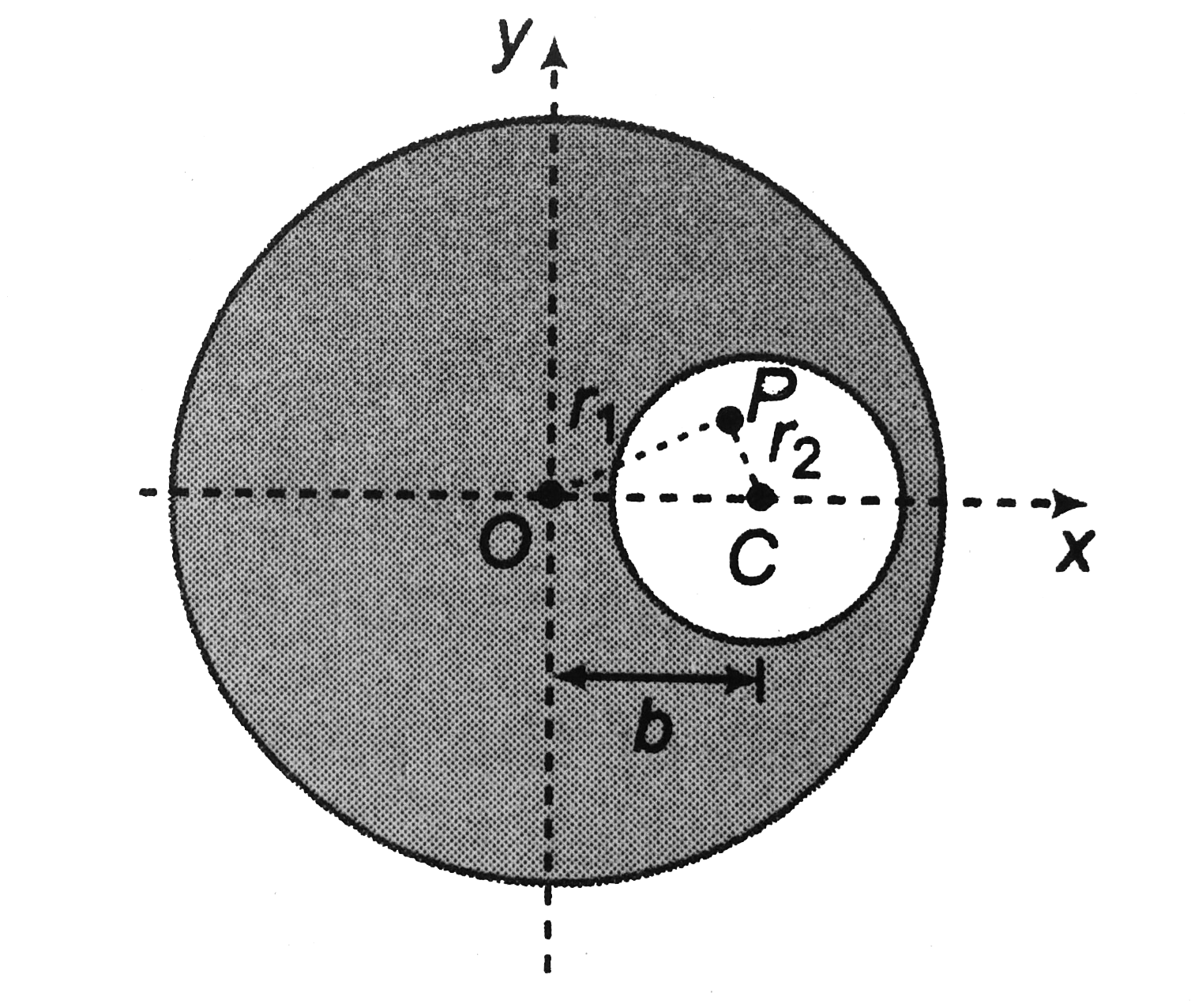
At point `P` magnetic field due to `i_1` is `B_1` (perpendicular to `OP`) and is `B_2` due to `i_2` (perpedicular to CP) in the directions shown. Although `B_1` and `B_2` are actually at P, but for better
understanding theey are drawnn at `O` and `C` respectively. Let `B_x` be the x-coponent of resultant of `B_1` and `B_2` and `B_y` its y-component. then
`B_x=B_1sinalpha-B_2sinbeta`
`=(mu_0/(2pi) i_1/(R^2)r_1)sinalpha-(mu_0/(2pi)i_2/alpha^2.r_2)sinbeta`
`=(mu_0/(2pi)(JpiR^2)/R^2.r_1sinalpha)-(mu_0/(2pi)(J.pia^2)/a^2r_2sinbeta)`
`(mu_0J)/2(r_1sinalpha-r_2sinbeta)=0`
Because in `/_\OPC r_1/(sinbeta)=r_2/(sinalpha)=h or r_1sinalpha-r_2sinbeta=0`
`Now, B_y=-(B-1cosalpha+B_2cosbet)`
`=-(mu_0J)/2(r_1cosalpha+r_2cosbeta)`
From `/_\OPC, "we can see that" `
`r_1cosalpha+r_2cosbeta=b or B_y=-(mu_0Jb)/2=`constant

Thus we can see that net magnetic field at point `P` is along negative y-direction and constant in magnitude.

