Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
INTERFERENCE AND DIFFRACTION OF LIGHT
DC PANDEY|Exercise Exercise 32.1|3 VideosINTERFERENCE AND DIFFRACTION OF LIGHT
DC PANDEY|Exercise Exercise 32.2|6 VideosINTERFERENCE AND DIFFRACTION OF LIGHT
DC PANDEY|Exercise Example Type 6|3 VideosGRAVITATION
DC PANDEY|Exercise All Questions|120 VideosMAGNETIC FIELD AND FORCES
DC PANDEY|Exercise Medical entrance s gallery|59 Videos
DC PANDEY-INTERFERENCE AND DIFFRACTION OF LIGHT-Miscellaneous Examples
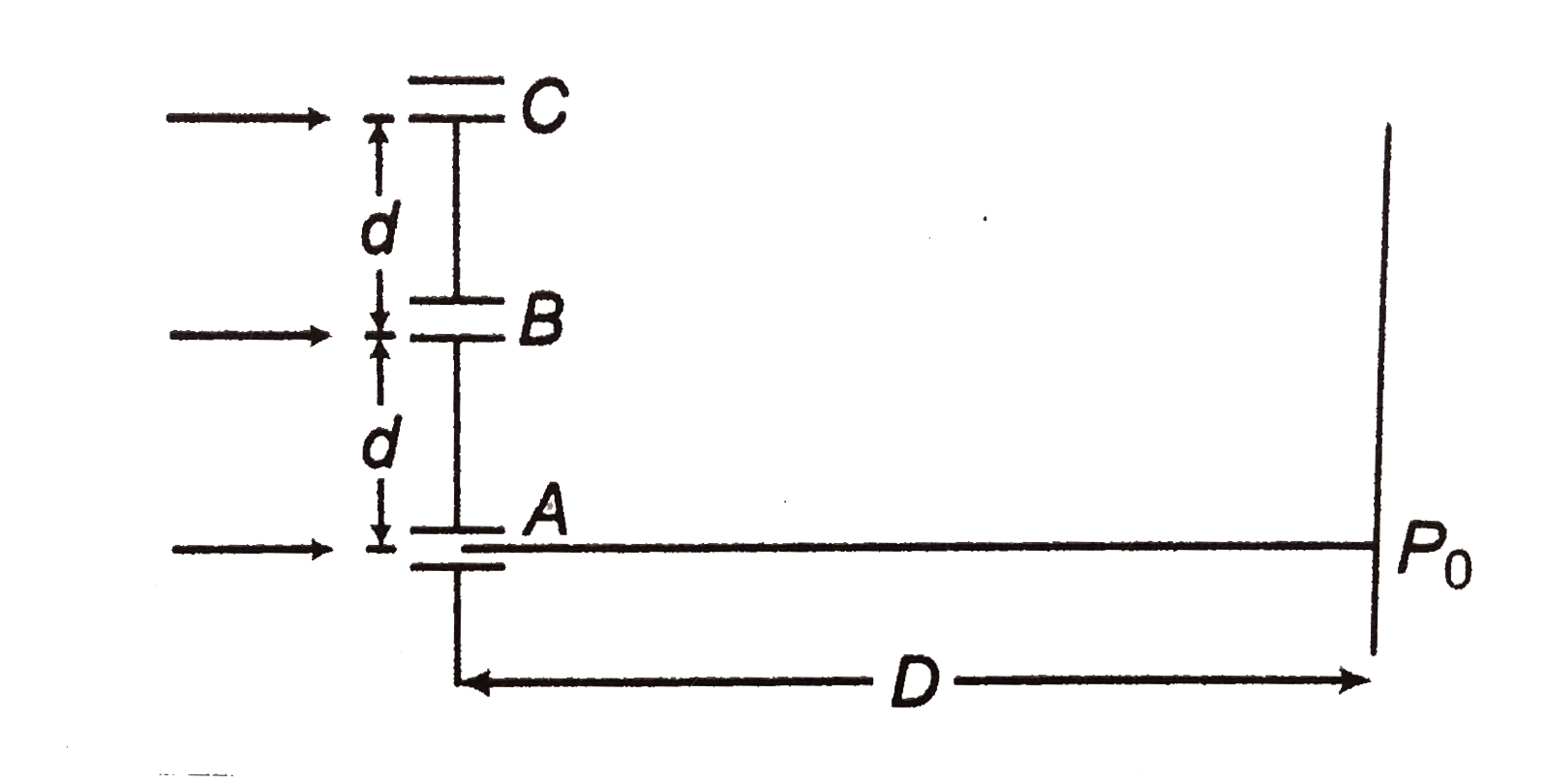
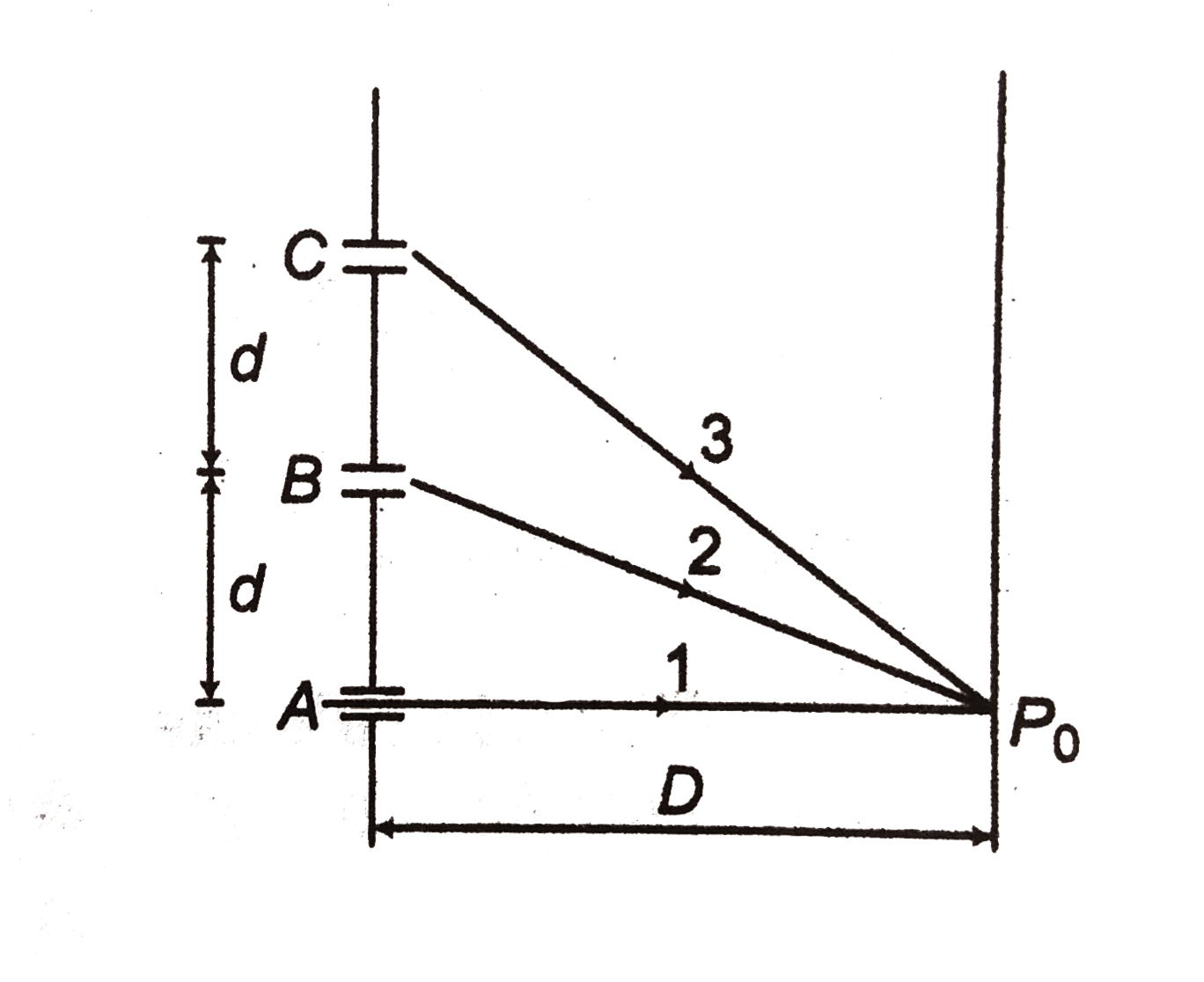
- figure shows three equidistant slits illuminated by a monochromatic pa...
Text Solution
|
- Young's double slit experiment is carried out using microwaves of wa...
Text Solution
|
- Two coherent sources are 0.3 mm apart. They are 0.9m away from the scr...
Text Solution
|
- In a Young's double slit set up, the wavelength of light used is 54nm....
Text Solution
|
- In a double slit pattern (lambda = 6000Å), the first order and tenth o...
Text Solution
|
- Two coherent narrow slits emitting light of wavelength lambda in the s...
Text Solution
|
- An interference is observed due to two coherent sources S1 placed at o...
Text Solution
|
- In a Young's double slit experiment, the light sources is at distance ...
Text Solution
|