Text Solution
Verified by Experts
|
Topper's Solved these Questions
THEOREMS
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise PYTHAGORAS THEOREM|4 VideosView PlaylistSTATISTICS
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise EXAMPLES FOR PRACTICE (MCQs)|35 VideosView PlaylistTRIGONOMETRY
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise CHALLENGING QUESTIONS|6 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
NAVNEET PUBLICATION - MAHARASHTRA BOARD-THEOREMS -CIRCLE
- Theorem:A line drawn through the end point of a radius and perpendicul...
04:52
|
Play - Theorem: The length of two tangents drawn from an external point to a ...
06:25
|
Play - If two circles touch each other (internally or externally); the point ...
02:45
|
Play - If two arcs of a circle (or of congruent circles) are congruent, then ...
01:47
|
Play - If two chords of a congruent circle are equal; then their correspondin...
05:55
|
Play - Inscribed Angle Theorem The measure of an inscribed angle is half ...
10:06
|
Play - Corollaries of inscribed angle theorem : Angle inscribed in the sa...
04:56
|
Play - In the figure, O is the centre of the circle. Seg AC is the diameter /...
01:40
|
Play - The sum of either pair of opposite angles of a cyclic quadrilateral is...
04:18
|
Play - Given : square ABCD is cyclic. /DCE is an exterior angle of ...
02:35
|
Play - If a line segment joining two points subtends equal angles at two othe...
05:53
|
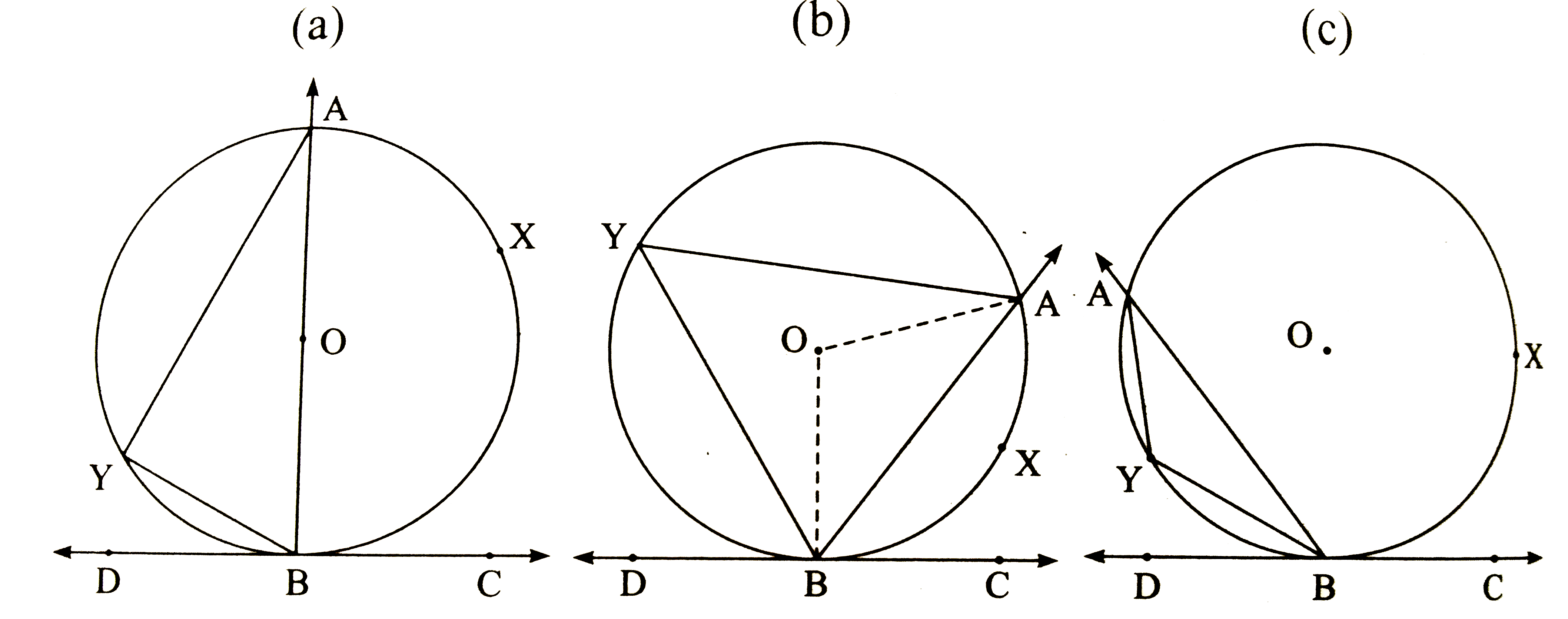
Play - Theorem of angle between tangent and secant If an angle has its ve...
08:57
|
Playing Now - Theorem of internal division of chords. Suppose two chords of a cir...
05:21
|
Play - Theorem of external division of chords. If secants containing chords...
05:48
|
Play - Tangent Secant Theorem Point E is in the exterior of a circle. A sec...
05:06
|
Play