Text Solution
Verified by Experts
|
Topper's Solved these Questions
DERIVATIONS-I
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Oscillations|5 VideosView PlaylistDERIVATIONS-I
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Elasticity|2 VideosView PlaylistDERIVATIONS-I
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Gravitation|7 VideosView PlaylistDEFINITIONS
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise COMMUNICATION SYSTEMS|3 VideosView PlaylistDERIVATIONS-II
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Assignments|9 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
NAVNEET PUBLICATION - MAHARASHTRA BOARD-DERIVATIONS-I-Rotational Motion
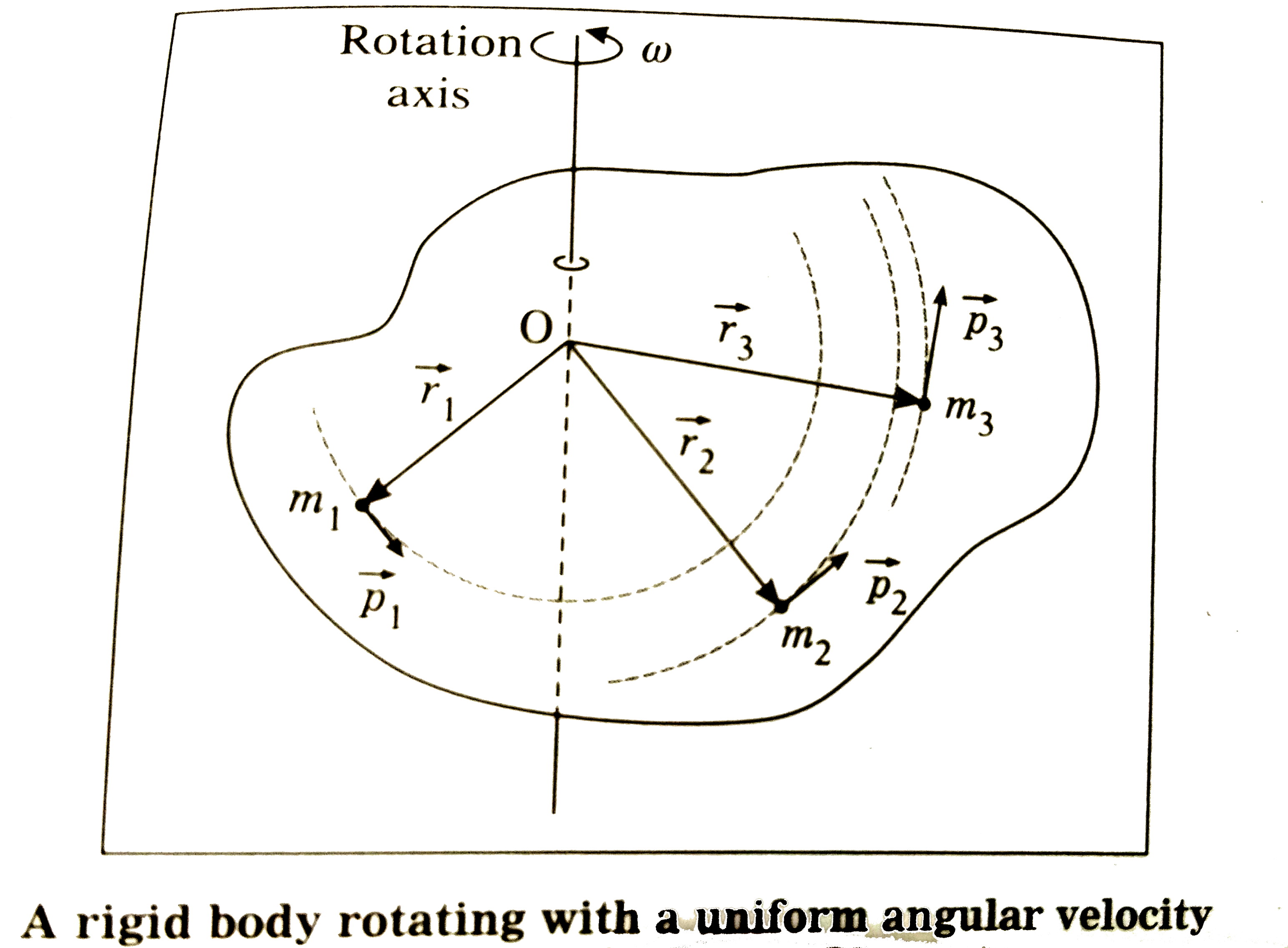
- For a body rotating with constant angular velcoity, its kinetic energy...
01:46
|
Play - Torque acting on a rotating body
03:57
|
Play - State and prove theorem of parallel axes.
06:58
|
Play - State and prove theorem of perpendicular axes.
03:50
|
Play - The moment of inertia of a thin uniform rod about an axis passing thro...
02:49
|
Play - Moment of inertia of a disc about its own axis is I. Its moment of ine...
02:23
|
Play - State the expression for the moment of inertia of a thin uniform disc ...
02:04
|
Play - A solid sphere rolls on horizontal surface without slipping. What is t...
01:31
|
Play - Obtain an expression for total kinetic energy of a rolling body in ...
06:34
|
Play - If a rigid bady of radius 'R' starts from rest and rolls down an incli...
06:16
|
Play - A hollow cylinder and a solid cylinder are rolling without slipping do...
07:00
|
Play - Establish a relation between angular momentum and moment of inertia of...
05:43
|
Play - Obtain an expression for torque acting on a rotating body with constan...
06:38
|
Playing Now