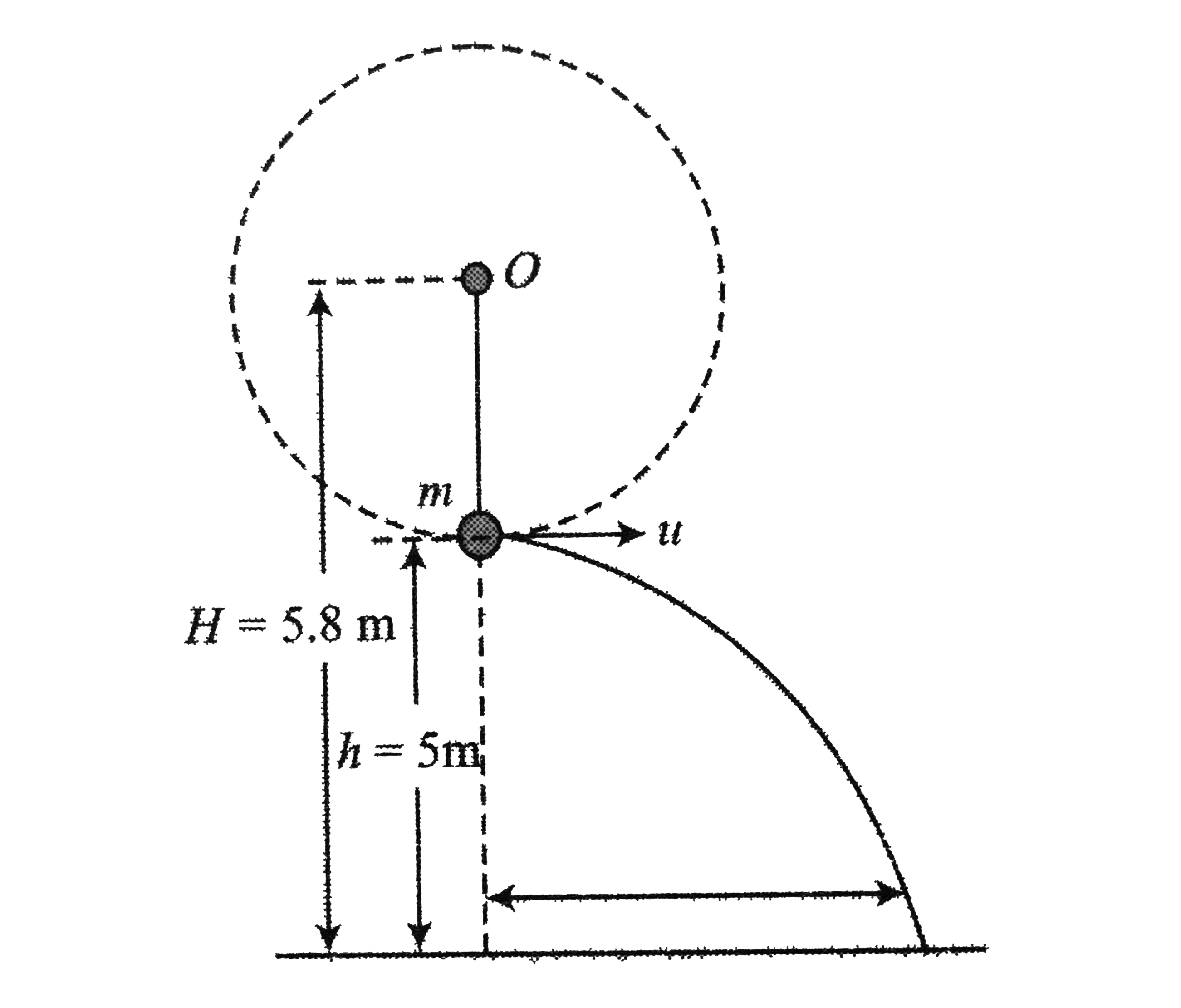
Text Solution
Verified by Experts
|
Topper's Solved these Questions
WORK, POWER & ENERGY
CENGAGE PHYSICS|Exercise Solved Examples|15 VideosView PlaylistWORK, POWER & ENERGY
CENGAGE PHYSICS|Exercise Exercise 8.1|25 VideosView PlaylistVECTORS
CENGAGE PHYSICS|Exercise Exercise Multiple Correct|5 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-WORK, POWER & ENERGY-Archives (integer)
- A small sphere tied to the string of length 0.8m is describing a verti...
08:59
|
Playing Now - A light inextensible string that gas over a smooth fixed pulley as sho...
04:51
|
Play - A block of mass 0.18 kg is attached to a spring of force-constant 2 N/...
05:36
|
Play - A bob of mass m, suspended by a string of length l1 is given a minimum...
03:17
|
Play - A particle of mass 0.2 kg is moving in one dimension under a force tha...
01:48
|
Play