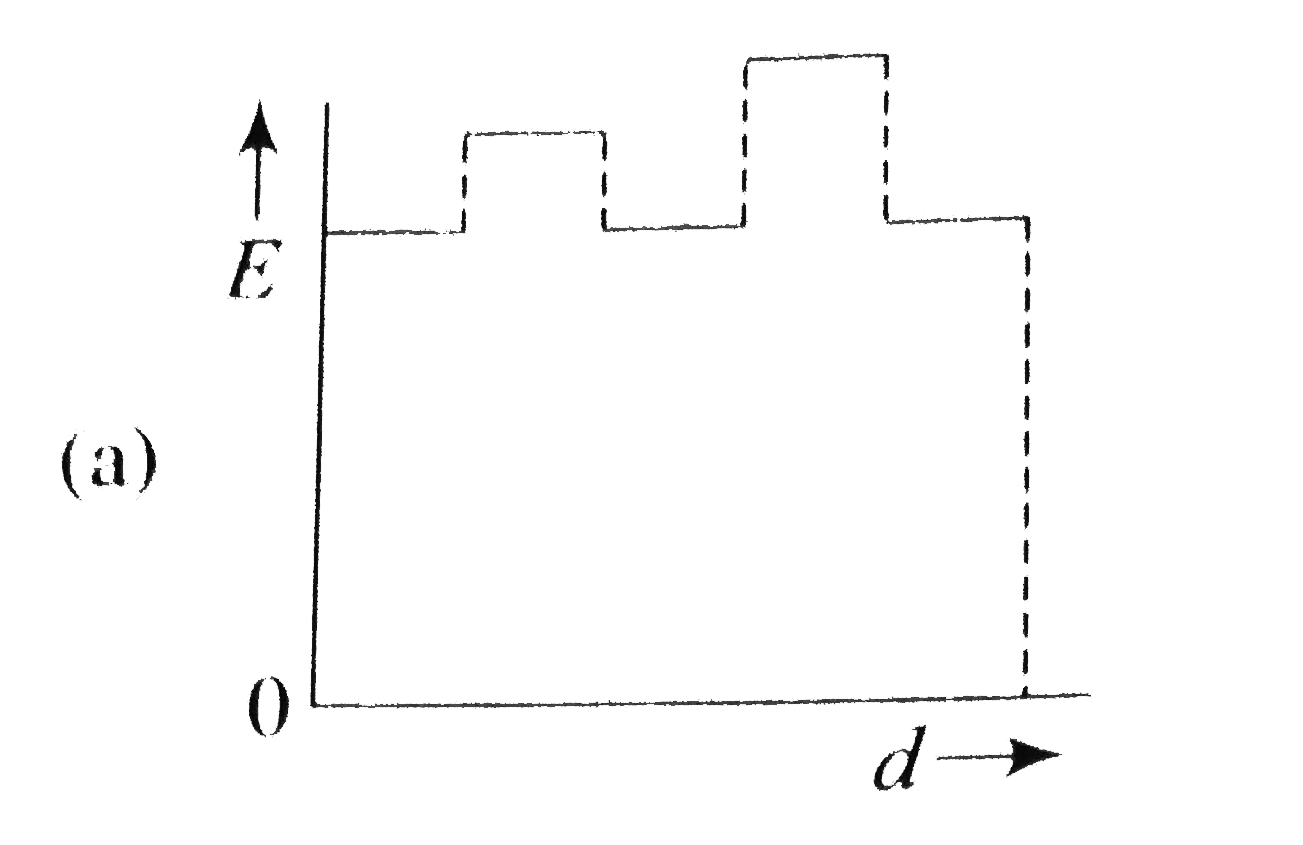
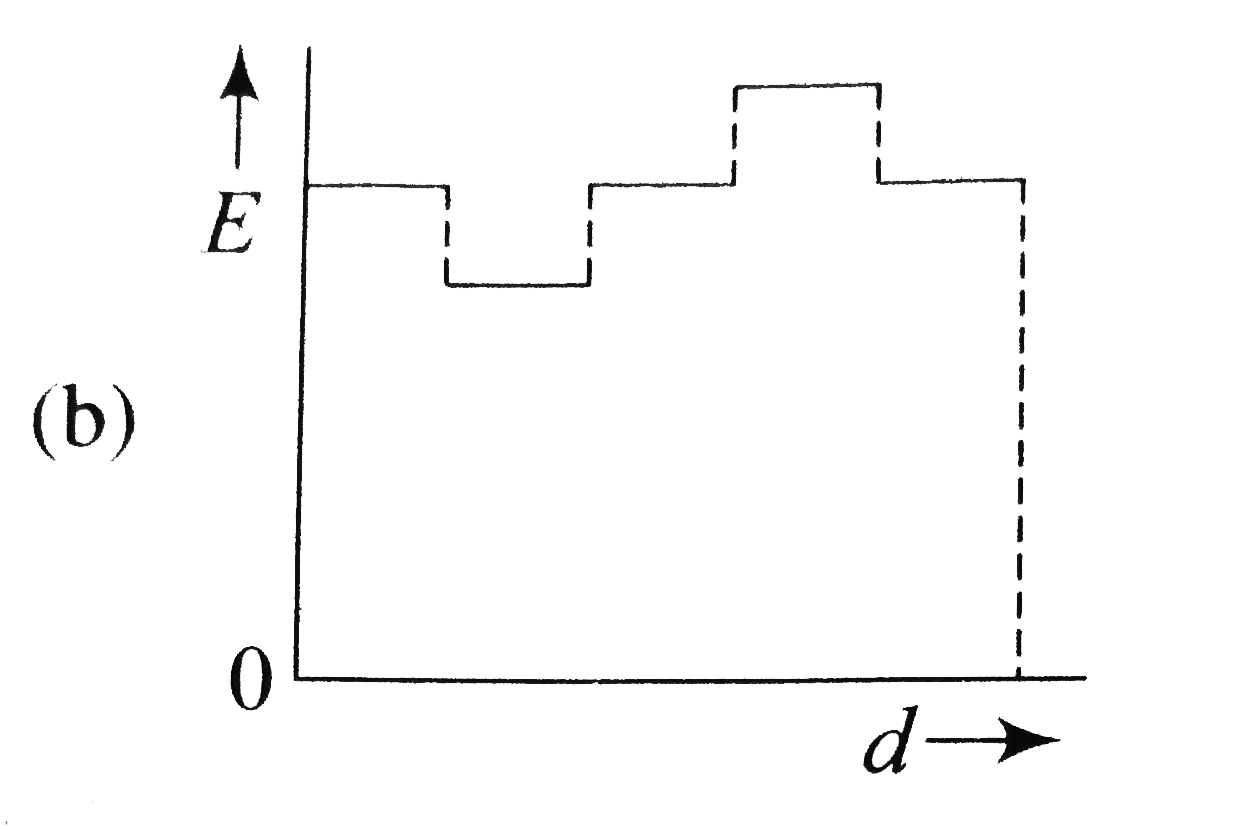
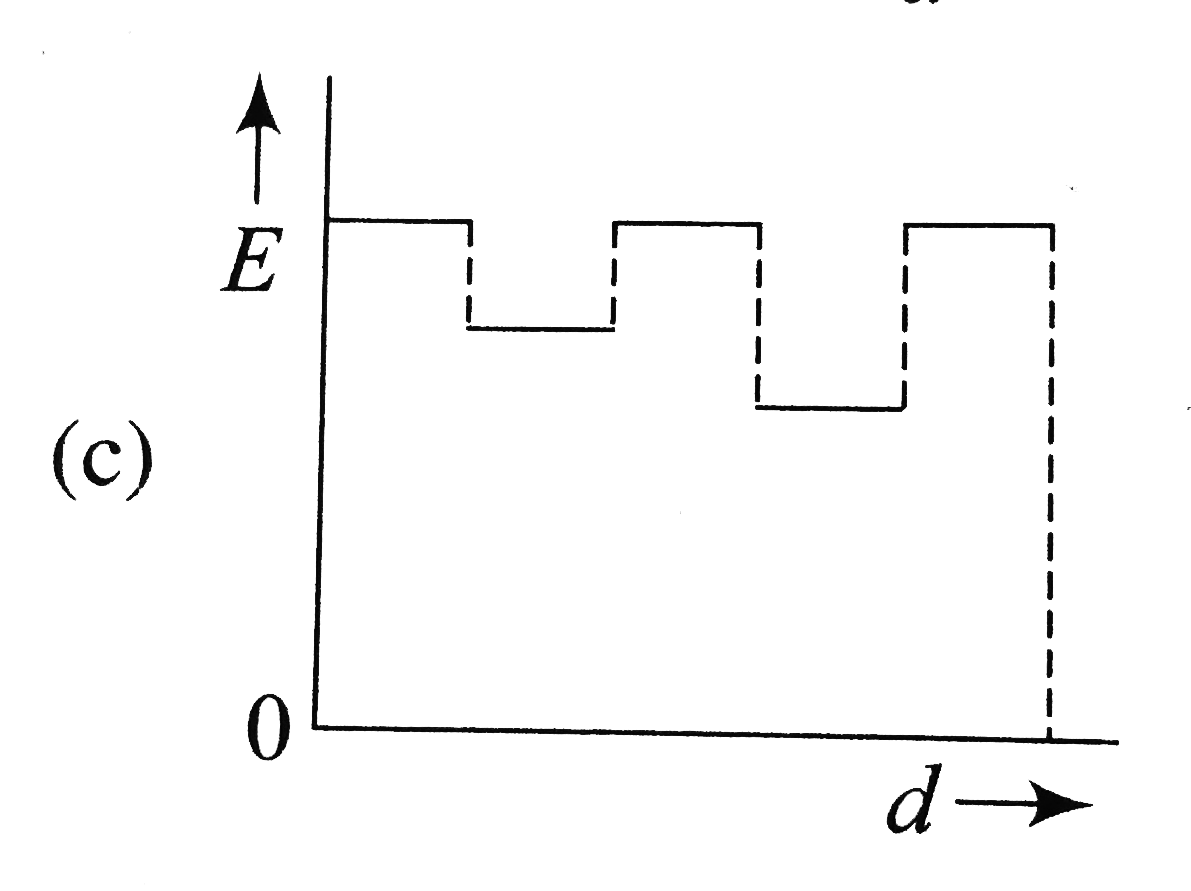
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
CAPACITOR AND CAPACITANCE
CENGAGE PHYSICS|Exercise Subjective|24 VideosView PlaylistCAPACITOR AND CAPACITANCE
CENGAGE PHYSICS|Exercise Single Correct|49 VideosView PlaylistCAPACITOR AND CAPACITANCE
CENGAGE PHYSICS|Exercise Exercise 4.1|13 VideosView PlaylistATOMS
CENGAGE PHYSICS|Exercise QUESTION BANK|40 VideosView PlaylistCENGAGE PHYSICS DPP
CENGAGE PHYSICS|Exercise subjective type|51 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-CAPACITOR AND CAPACITANCE-Exercise 4.2
- Find whether the following statements are true or false. a. If a bat...
04:12
|
Play - Find the equicalent capacitance between points A and B as show in .
01:19
|
Play - Three capacitors C(1),C(2) and C(3) are connected as shown in, The pot...
02:24
|
Play - Find the charge supplied by the battery in the arrangement as shown in...
01:44
|
Play - Two large parallel metal plates, each having area A, are oriented hori...
02:17
|
Play - A 10 muF capacitor is charged to 15 V. It is next connected in seties ...
02:33
|
Play - Consider the situation shown in figure (31-E23 ) . The switch S is ope...
04:20
|
Play - Figure shows two identical parallel plate capacitors connected to a sw...
05:47
|
Play - Four parallel large plates separated by equal distance d are arranged ...
03:40
|
Play - Find the charges on the three capacitors shown in figure
05:40
|
Play - Four capacitors C(1)=8 muF, C(2)=2 muf, C(3)=6 muF, and C(4)=6, muF ...
04:10
|
Play - Three capacitors of capacitances 1 muF, 2 muF, and 2 muF, are cahrged ...
04:09
|
Play - Three initially uncharged capacitors are arranged with batteries as sh...
03:11
|
Play - A capacitor of capacitance C which is initially charged up to a poten...
01:17
|
Play - A 5.0muF capacitor is charged to 12V. The positive plate of this capac...
08:14
|
Play - Find the capacitance between A and B if two dielectric alabs (each of ...
02:26
|
Playing Now - Find the capacitance between A and B if two dielectric slabs (each of ...
02:11
|
Play - Find the capacitance between A and B if three dielectric slabs of diel...
03:29
|
Play - Three dielectrics of relative permittivities epsilon(r(1))=1,epsilon(r...
02:47
|
Play - T Two capacitors of capacitances 1 muF and 2 muF are charged to potent...
02:16
|
Play
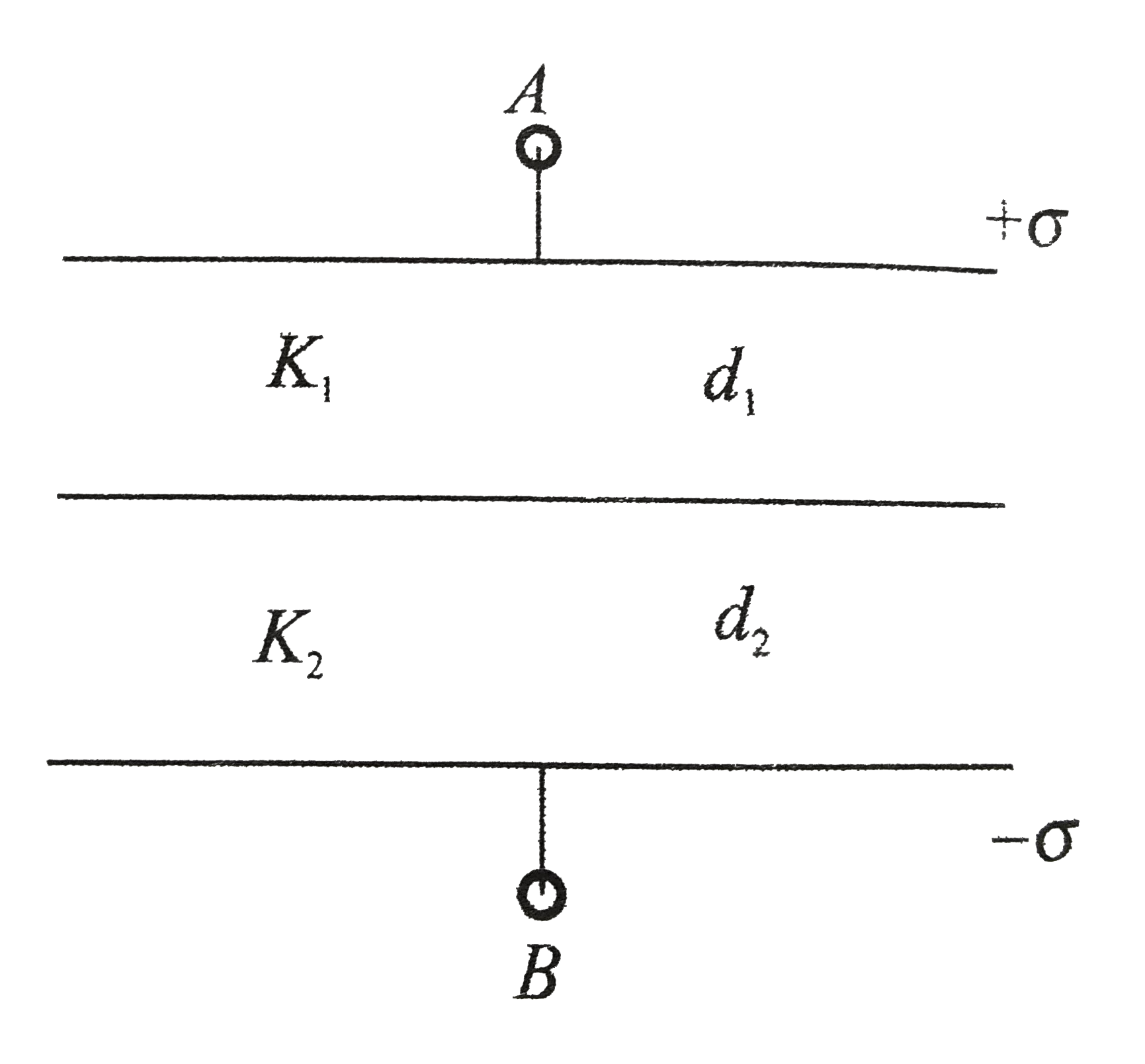 .
.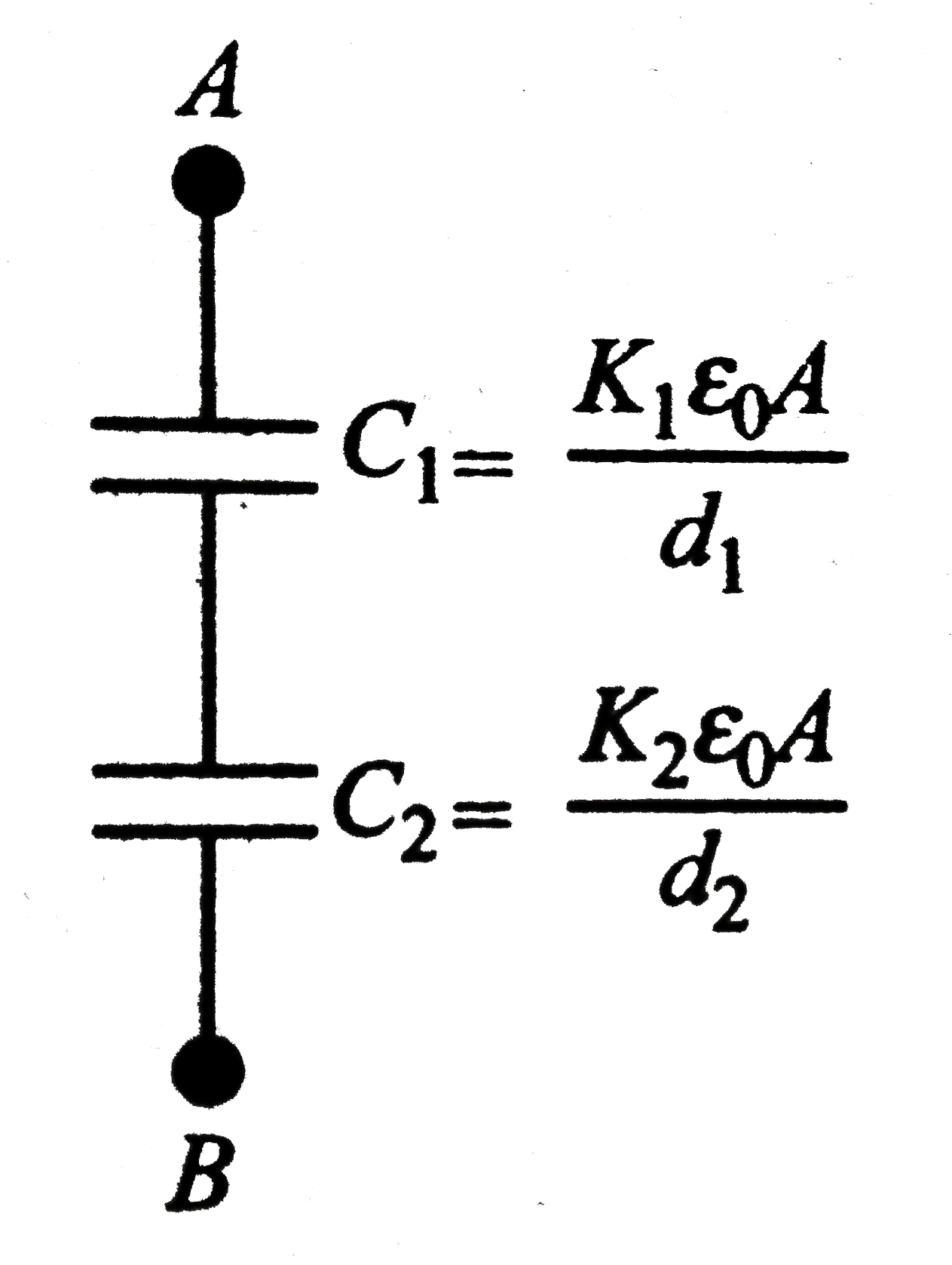 .
.