Home
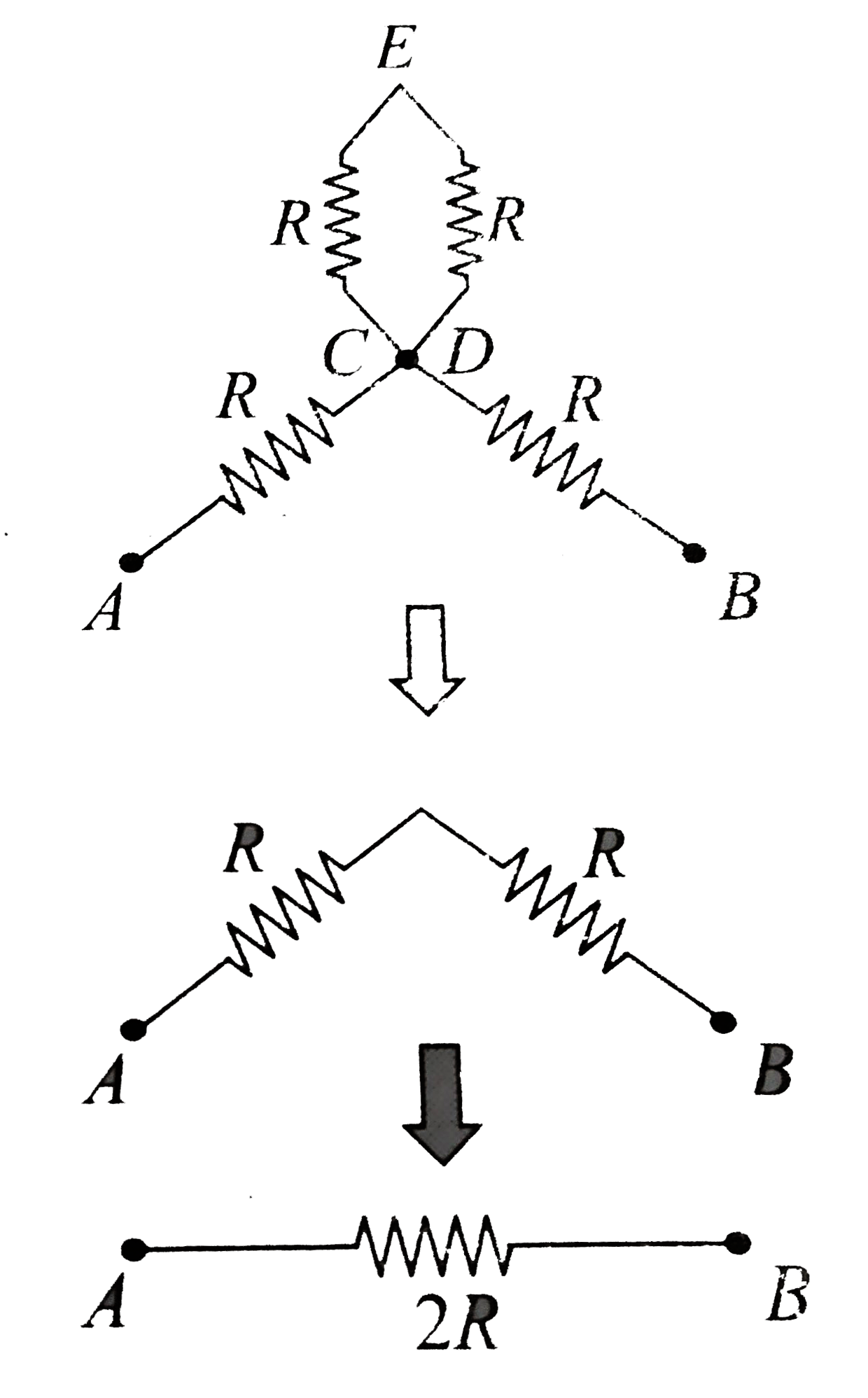
Class 12
PHYSICS
Four identical resistances each having v...

Four identical resistances each having value R are arranged as shown in Figure. Find the equivalent resistance between A and B.

A

R

B

2R

C

3R

D

4R

Text Solution

Verified by Experts

The correct Answer is:
B
Since C and D are conneted with
a zero resistor, they are equipotential.
Then superimpose C and D to obtain
the simplified circuit as shown. Since no
current flows in the branches CE and ED
cut and then thro them to have
`R_(AB) =R + R = 2R`
If we get a closed loop of resistors
without any battery, it carries no current
Then remove the total loop to get a
simpler circuit or if the current in any
branch is zero, remove it.
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • ELECTRIC CURRENT AND CIRCUIT

    CENGAGE PHYSICS|Exercise Solved Examples|12 Videos

  • ELECTRIC CURRENT AND CIRCUIT

    CENGAGE PHYSICS|Exercise Exercise 5.1|28 Videos

  • ELECTRIC CURRENT & CIRCUITS

    CENGAGE PHYSICS|Exercise Kirchhoff s law and simple circuits|15 Videos

  • ELECTRIC FLUX AND GAUSS LAW

    CENGAGE PHYSICS|Exercise MCQ s|38 Videos

Similar Questions

Explore conceptually related problems

Each resistance is of 1Omega in the circuit diagram shown in figure. Find out equivalent resistance between A and B.

Four identical plates, each having area A, are arranged as shown in Fig. Find the equicalent capacity of the structure between (A) and (B). .

Knowledge Check

  • Three equal resistances each of value R are joined as shown in the figure. The equivalent resistance between M and N is

    A
    R
    B
    2R
    C
    `(R)/(2)`
    D
    `(R)/(3)`

  • Five resistance, each of 5Omega are connected as shown in figure. Find the equivalent resistance between points (1) A and B , (2) A and C .

    A
    (1) `7.5Omega` (2) `2.25Omega`
    B
    (1) `5Omega` (2) `2.50Omega`
    C
    (1) `2.5Omega` (2) ` 3.13Omega`
    D
    (1) `3Omega` (2) `2.5Omega`

  • For infinite ladder network containing identical resistance of R Omega each, are combined as shown in figure. The equivalent resistance between A and B is R_(AB) and between A and C is R_(AC) . Then the value (R_(AB))/(R_(AC)) is :

    A
    `(3)/(4)`
    B
    `(4)/(3)`
    C
    2
    D
    `(1)/(2)`

    • Similar Questions

    Explore conceptually related problems

    Idnetical resistor each of resistance r are connected as shown in figure. Calculate equivalent resistance between A and E.

    Four identical resistances are joined as shown in the figure. The equivalent resistance between points A and B is R_(1) and that between A anc C is R_(2) then ratio R_(1)//R_(2) is

    Each resistance shown in figure is 2 Omega . The equivalent resistance between A and B is

    Each of the resistor shown in fig. has resistance R. Find the equivalent resistance between A and B

    Three equal resistors, each equals to r are connected as shown in figure. Then, the equivalent resistance between points A and B is

    Home
    Profile