A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Assertion Reasoning|6 VideosLINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Comprehension|33 VideosLINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Single Correct|107 VideosKINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
CENGAGE PHYSICS|Exercise Interger|11 VideosMISCELLANEOUS KINEMATICS
CENGAGE PHYSICS|Exercise Interger type|3 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Multiple Correct
- A coin is placed on a horizontal platform which undergoes vertical sim...
Text Solution
|
- For a simple harmonic motion with given angular frequency omega, two a...
Text Solution
|
- The potential energy U of a body of unit mass moving in one dimensiona...
Text Solution
|
- For the spring pendulum shown in fig. the value of spring constant is ...
Text Solution
|
- An object of mass m is performing simple harmonic motion on a smooth h...
Text Solution
|
- A simple pendulum consists of a bob of mass m and a light string of le...
Text Solution
|
- A particle performing simple harmonic motion undergoes unitial displac...
Text Solution
|
- A particle is subjected to two simple harmonic motions along x and y d...
Text Solution
|
- The speed v of a particle moving along a straight line, when it is at ...
Text Solution
|
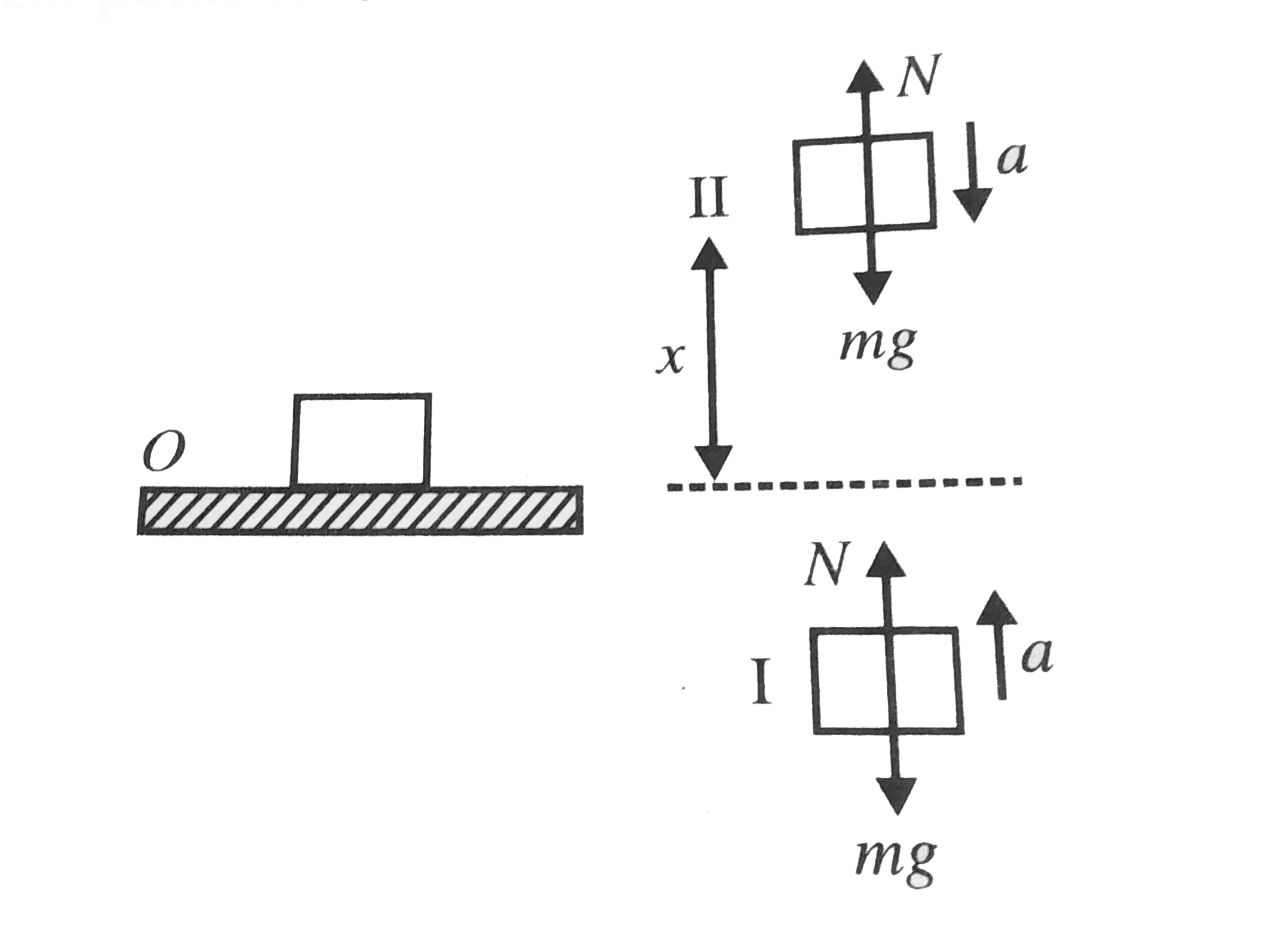
- A horizontal plank has a rectangular block placed on it. The plank sta...
Text Solution
|
- A 20g particle is subjected to two simple harmonic motions x1=2sin10t,...
Text Solution
|
- A spring block system undergoes SHM on a smooth horizontal surface, th...
Text Solution
|
- The potential energt of a particle of mass 0.1 kg, moving along the x-...
Text Solution
|
- The time period of a particle in simple harmonic motion is T. Assume p...
Text Solution
|
- Figure. (a) shows a spring of force constant k fixed at one end and ca...
Text Solution
|
- When the point of suspendion of pendulum is moved, its period of oscil...
Text Solution
|
- The displacement time relation for a particle can be expressed as y=0....
Text Solution
|
- At two particular closest instant of time t1 and t2 the displacements ...
Text Solution
|
- Two blocks connected by a spring rest on a smooth horizontal plane as ...
Text Solution
|
- A block of mass m is suspended by a rubber cord of natural length l=(m...
Text Solution
|