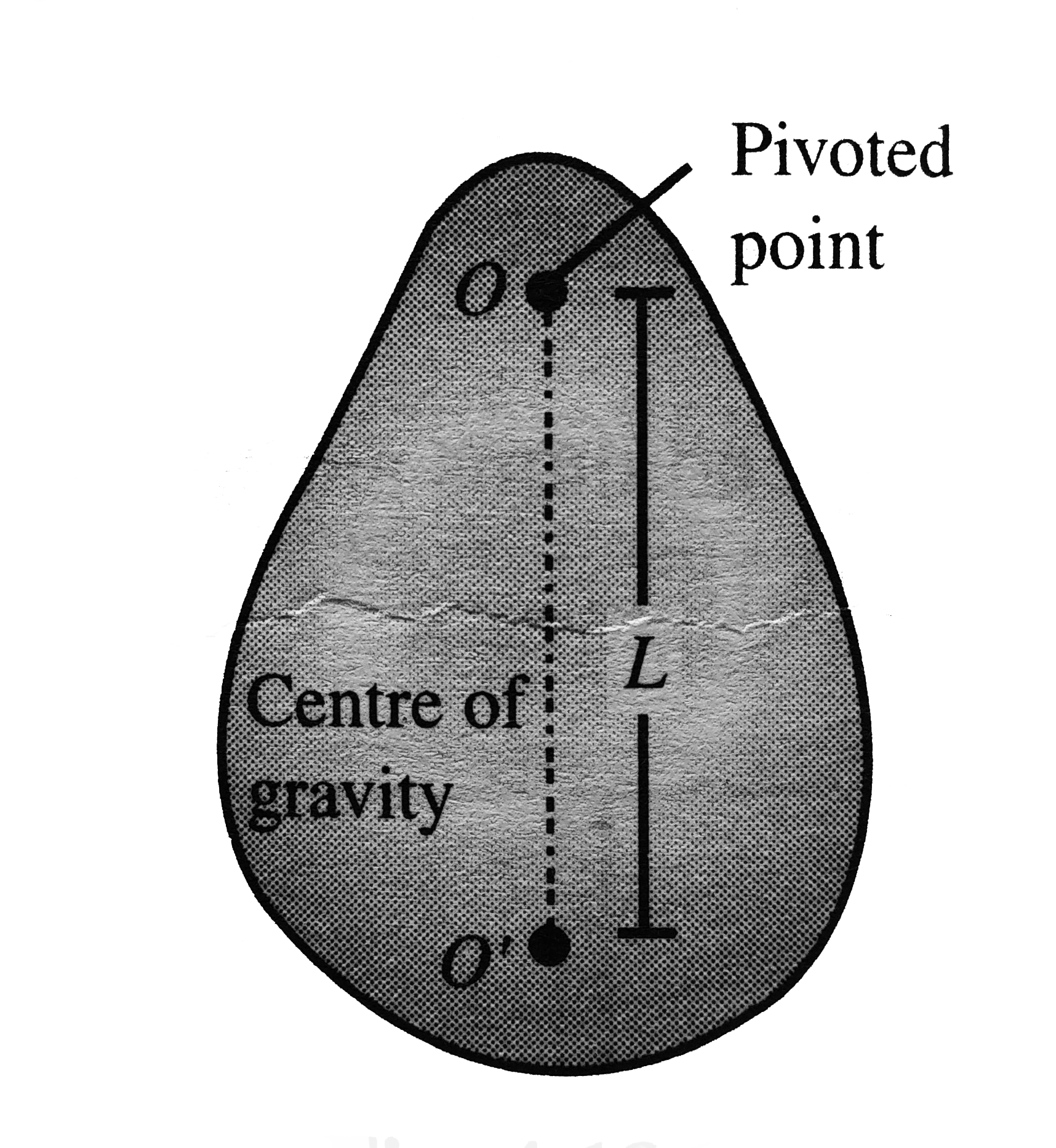
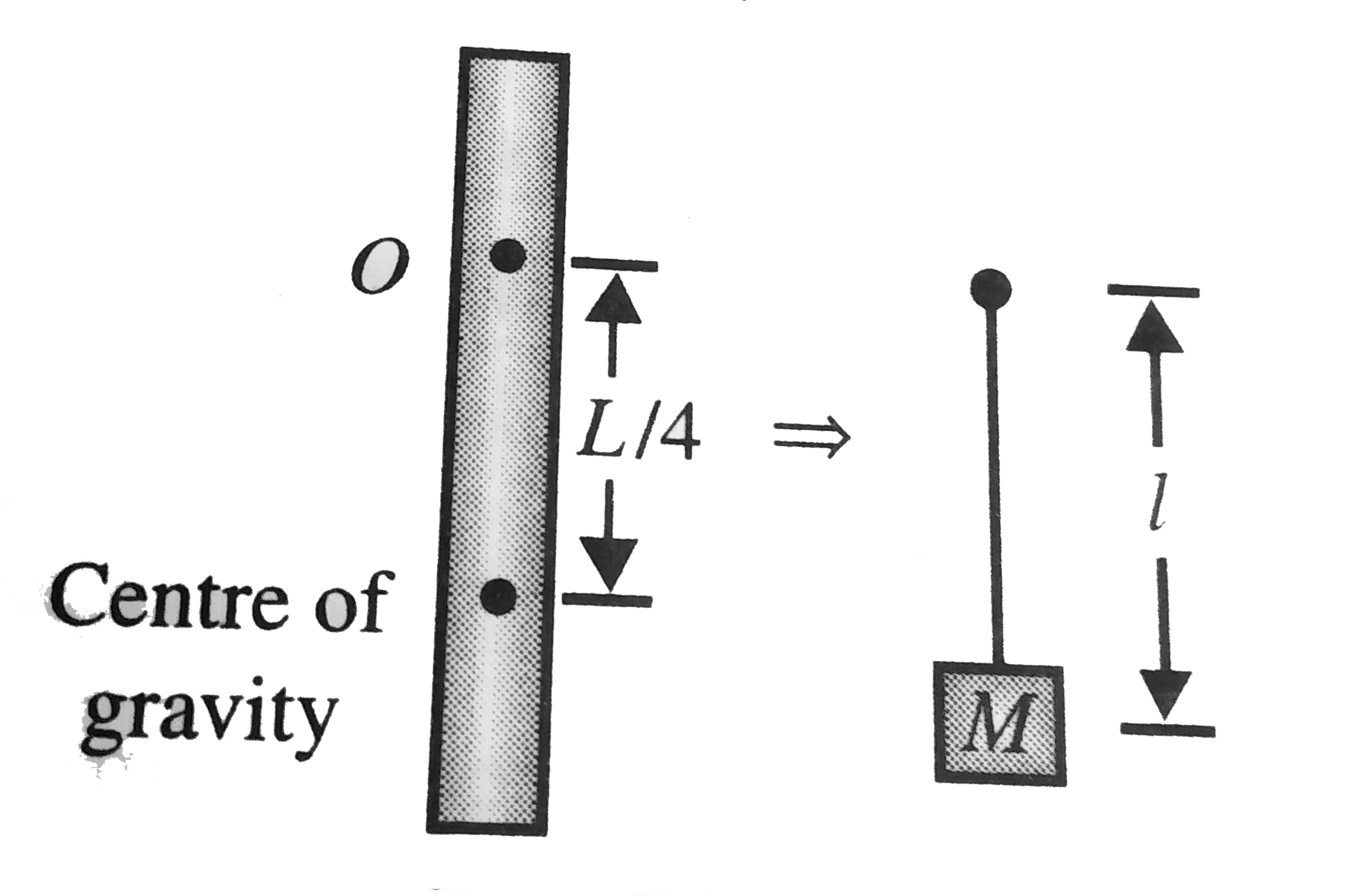
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Integer|10 VideosView PlaylistLINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Subjective type|2 VideosView PlaylistLINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Assertion Reasoning|6 VideosView PlaylistKINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
CENGAGE PHYSICS|Exercise Interger|11 VideosView PlaylistMISCELLANEOUS KINEMATICS
CENGAGE PHYSICS|Exercise Interger type|3 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Comprehension
- A block of mass m is connected to a spring of spring constant k as sho...
05:37
|
Play - A block of mass m is connected to a spring of spring constant k as sho...
05:37
|
Play - In physical pendulum, the time period for small oscillation is given b...
09:56
|
Playing Now - In physical pendulum, the time period for small oscillation is given b...
09:56
|
Play - In physical pendulum, the time period for small oscillation is given b...
09:56
|
Play - A block of mass m is suspended from one end of a light spring as shown...
19:29
|
Play - A block of mass m is suspended from one end of a light spring as shown...
19:29
|
Play - A block of mass m is suspended from one end of a light spring as shown...
19:29
|
Play - Two identical blocks A and B, each of mass m=3kg, are connected with t...
18:21
|
Play - Two identical blocks A and B, each of mass m=3kg, are connected with t...
18:21
|
Play - Two identical blocks A and B, each of mass m=3kg, are connected with t...
18:21
|
Play - A small block of mass m is fixed at upper end of a massive vertical sp...
13:19
|
Play - A small block of mass m is fixed at upper end of a massive vertical sp...
13:19
|
Play - A small block of mass m is fixed at upper end of a massive vertical sp...
13:19
|
Play - A 100 g block is connected to a horizontal massless spring of force co...
13:32
|
Play - A 100 g block is connected to a horizontal massless spring of force co...
13:32
|
Play - A 100 g block is connected to a horizontal massless spring of force co...
13:32
|
Play - A 100 g block is connected to a horizontal massless spring of force co...
13:32
|
Play - A 100 g block is connected to a horizontal massless spring of force co...
13:32
|
Play - A spring having a spring constant k is fixed to a vertical wall as sho...
07:40
|
Play