Electric potential (V): The workdone by a unit positive charge from infinite to a point in an electric field called electric potentials.
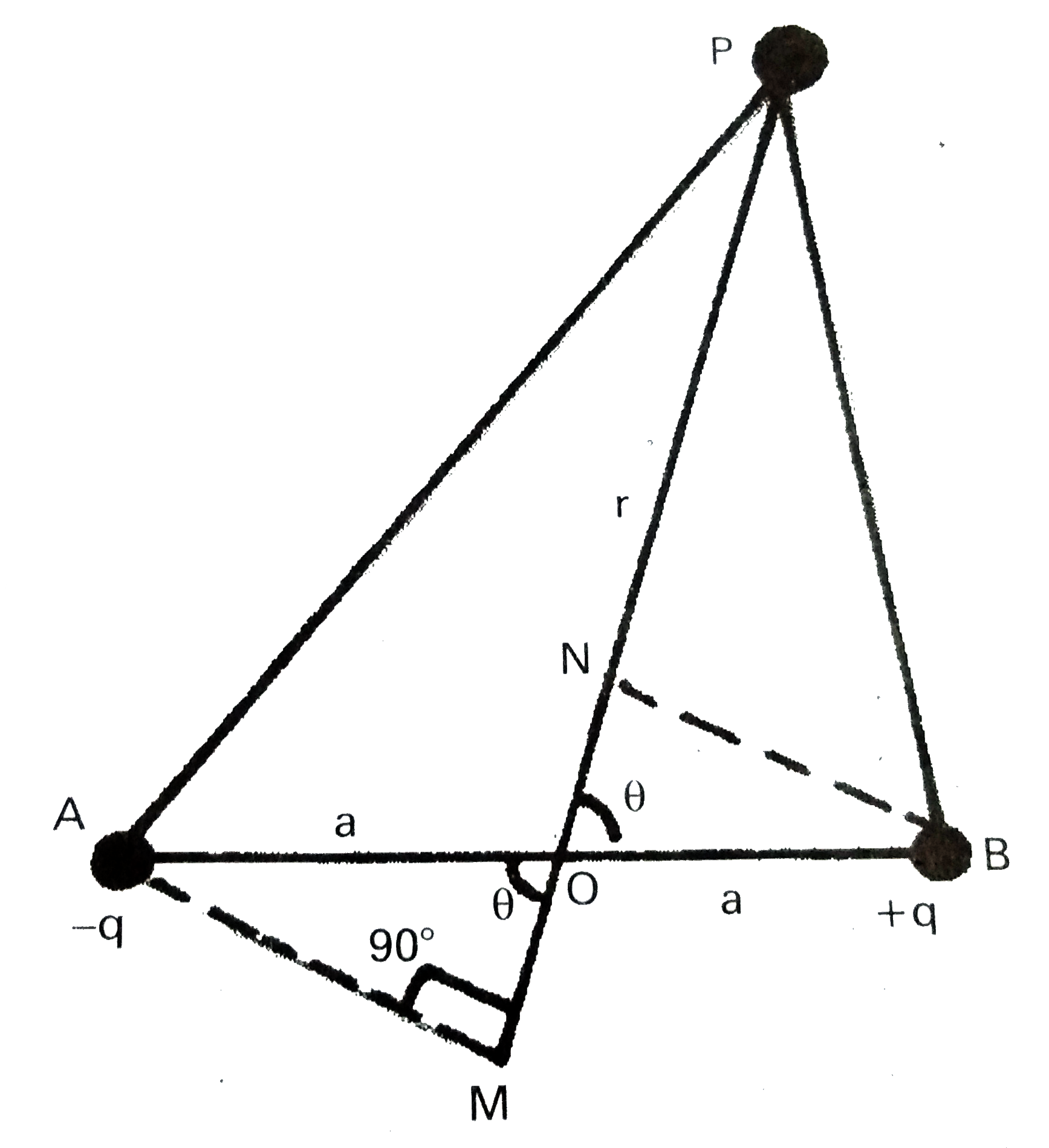
1. Consider A and B having -q and +q charges separated by a distance 2a.
2. The electric dipole moment `P=qxx2a` along AB.
3. The electric potential at the point 'P' is to be calculated.
4. P is at a distance 'r' from the point 'O'. `theta` is the angle between the line OP and AB.
5. BN and AM are perpendicular to OP.
7. Potential at P due to charge `-q at A, V_2=(1)/(4 pi epsi_0)[(-q)/(AP)]`
`therefore V_1=(1)/(4pi epsi_0)[(-q)/(MP)][because AP=MP]`
8. Therefore , Resultant potential at P is `V=V_1+V_2`
`V=(1)/(4piepsi_0)[(q)/(NP)-(q)/(MP)]`..............(1)
9. In `Delta le ONB,ON=OB cos theta =a cos theta, therefore NP=OP -ON=r-a cos theta`............(ii)
10. In `Delta le AMO,OM=AO cos theta=a cos theta, therefore MP=MO+OP=r+a cos theta`............(3)
11. Substituting (2) and (3) in (1) , we get
`V=(1)/(4 pi epsi_0)[(q)/(r-a cos theta)-(q)/(r+acos theta)]=(q)/(4 pi epsi_0)[(2acos theta)/(r^2-a^2cos^2theta)]`
`therefore V=(P cos theta)/(4pi epsi_0(r^2-a^2cos^2theta))[because P=2aq]`
12. As ` r gt gt a , a ^2cos^2 theta` can be neglected with comparision of `r^2`.
`therefore V=(Pcos theta)/(4pi epsi_0r^2)`
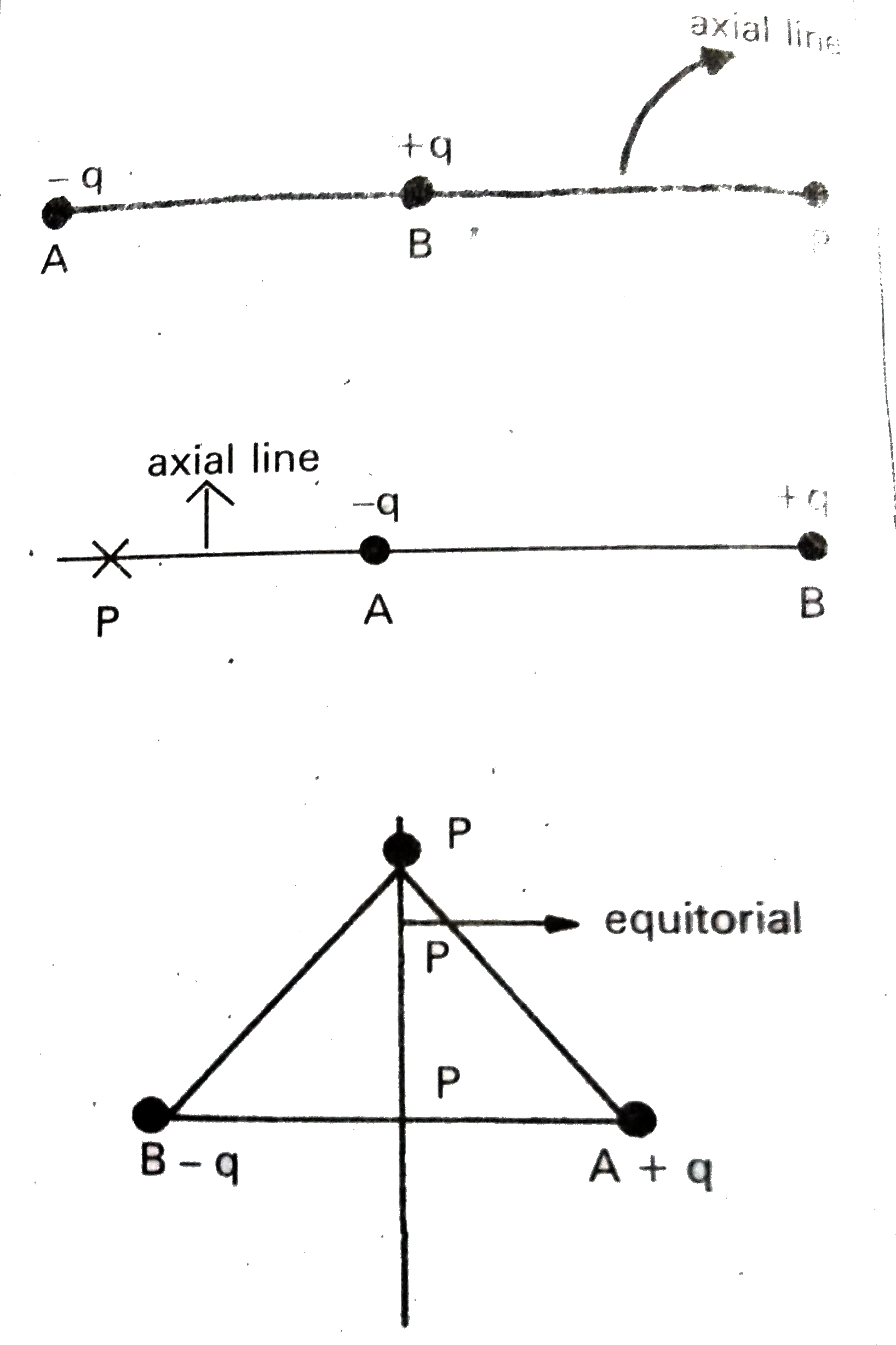
13. (a) Electric potential on the axial line of dipole :
(i) When `theta=0^@`. Point p line on the side of `+q`
`therefore V=(P)/(4piepsi_0r^2) [because cos 0^@=1]`
(ii) When `theta=180^@`, point p lies on the side of -q .
`therefore V=(-P)/(4piepsi_0r^2) [because cos 180^@=-1]`
(b) Electric potential on the equitorial ine of the dipole :
when `theta=90^@`, point P lies on the equitorial line.
`therefore V=0 [ because cos 90^@=0]`.