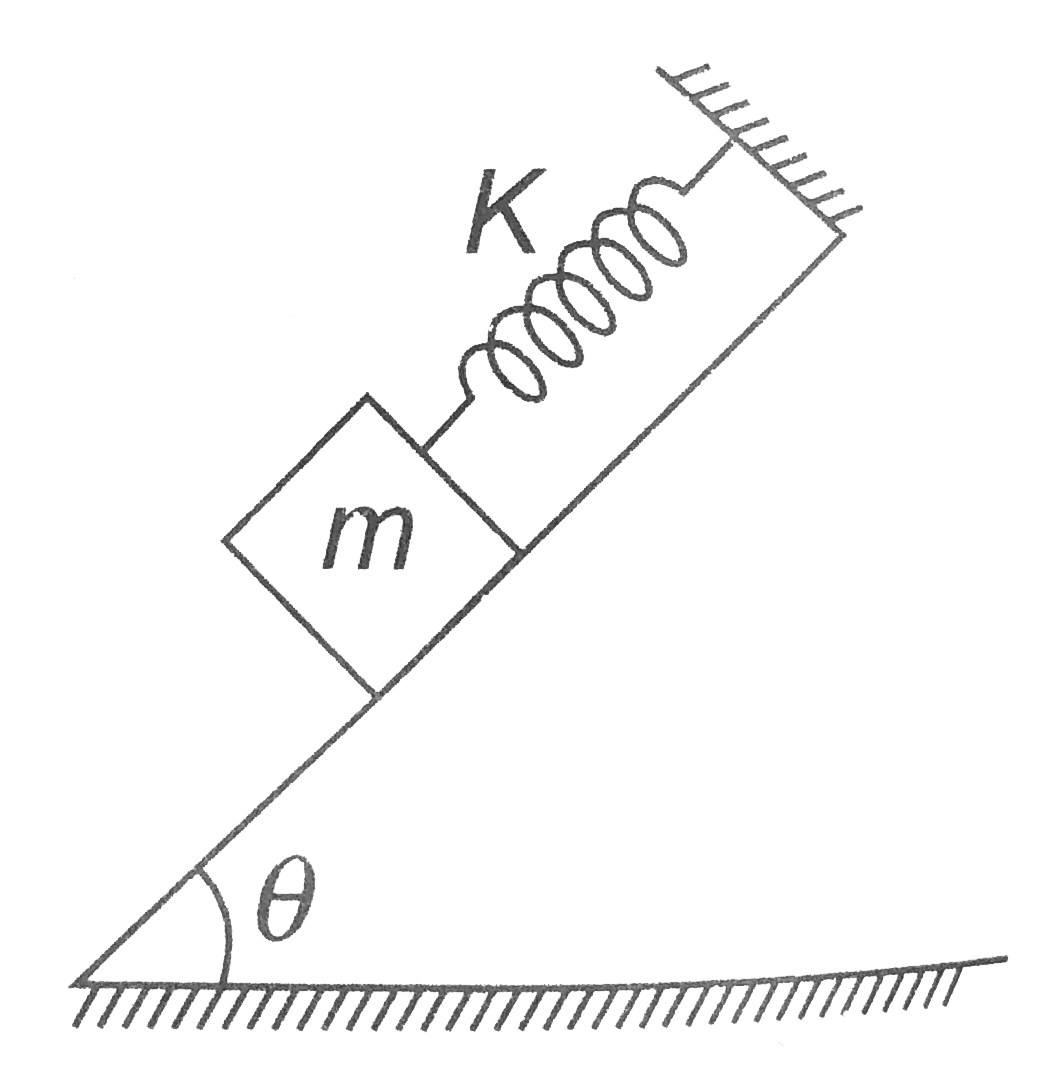
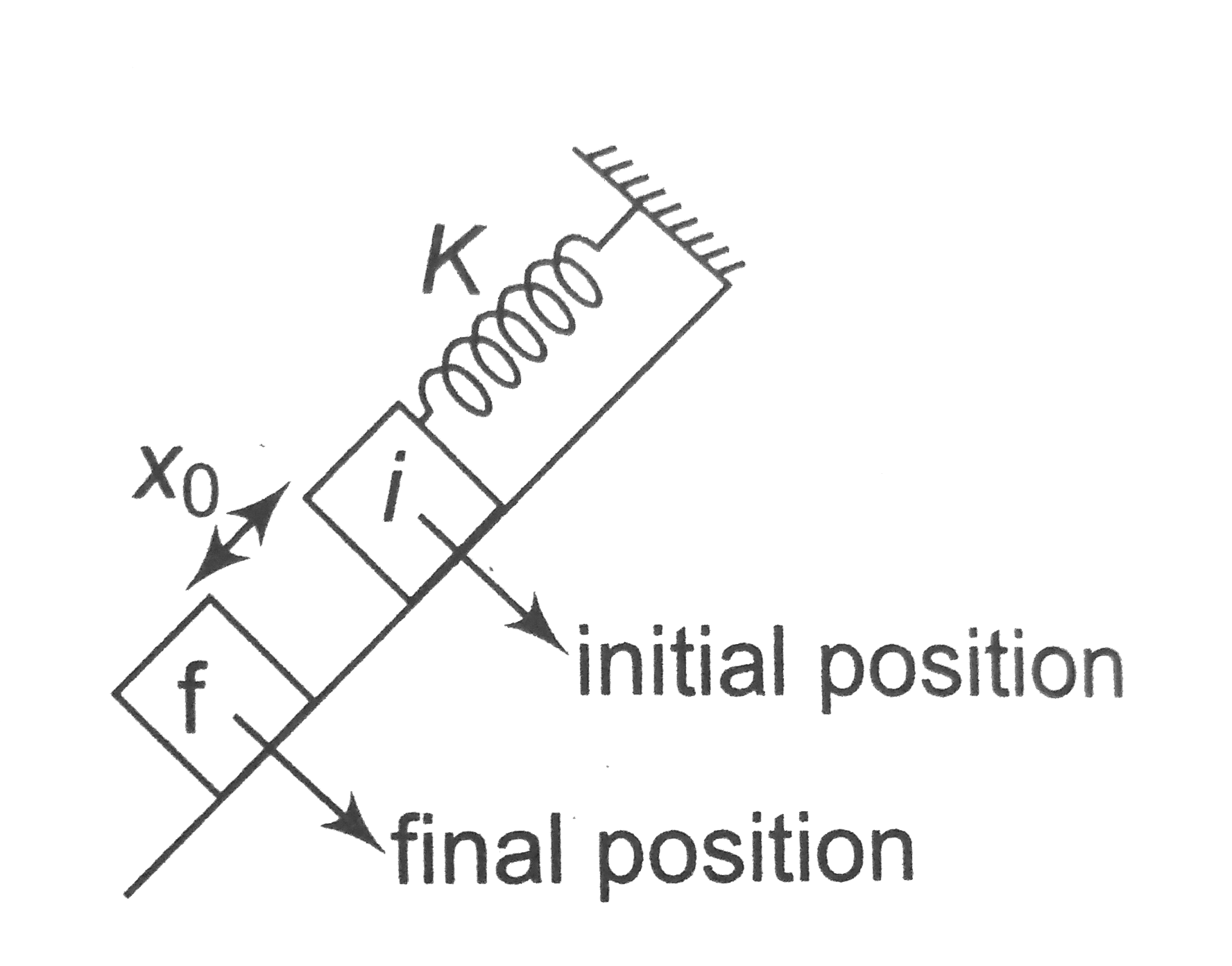
A
B
C
D
Text Solution
Verified by Experts
|
Topper's Solved these Questions
WORK, ENERGY, POWER AND COLLISION
A2Z|Exercise AIIMS Questions|20 VideosView PlaylistWAVES AND ACOUSTICS
A2Z|Exercise Chapter Test|30 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
A2Z-WORK, ENERGY, POWER AND COLLISION-Chapter Test
- A block is moved from rest through a distance at 4 m along a string li...
02:23
|
Play - An object of mass m is allowed to fall from rest along a rough inclin...
02:29
|
Play - Given that the position of the body in m is a function of time as foll...
01:39
|
Play - If v be the instantaneous velocity of the body dropped from the top of...
01:05
|
Play - Two springs have their force constant as k(1) and k(2) (k(1) gt k(2))...
01:48
|
Play - The power of a water pump is 2 kW. If g = 10 m//s^2, the amount of wat...
00:59
|
Play - Water is flowing in a river at 2 ms^(-1). The river is 50 m wide and h...
05:44
|
Play - The potential energy of a partical veries with distance x as shown in ...
00:49
|
Play - Which of the following graph is correct between kinetic energy E, pote...
04:35
|
Play - A ball hits a floor and rebounds after an inelastic collision. In this...
01:29
|
Play - The graph between the resistive force F acting on a body and the dista...
02:05
|
Play - In the figure shown, a spring of spring constant K is fixed at on end...
04:49
|
Playing Now - Two identical balls A and B are released from the position shown in Fi...
07:25
|
Play - Two equal sphere A and b lie on a smooth horizontal circle groove at o...
02:56
|
Play - Two bodies of mass m and 4m are attached with string of length l is ex...
03:43
|
Play - A ball of mass m moving with velocity vecu = u(x) hati + u(y) hatj hit...
02:37
|
Play - A set of a identical cubical blocks lies at rest parallel to each othe...
02:47
|
Play - Assertion : For two bodies, the sum of the mutual forces exerted betwe...
01:31
|
Play - Assertion: According to law of conservation of machainical energy chan...
01:05
|
Play - Assertion : The work done by the spring force in a cyclic process is z...
01:03
|
Play