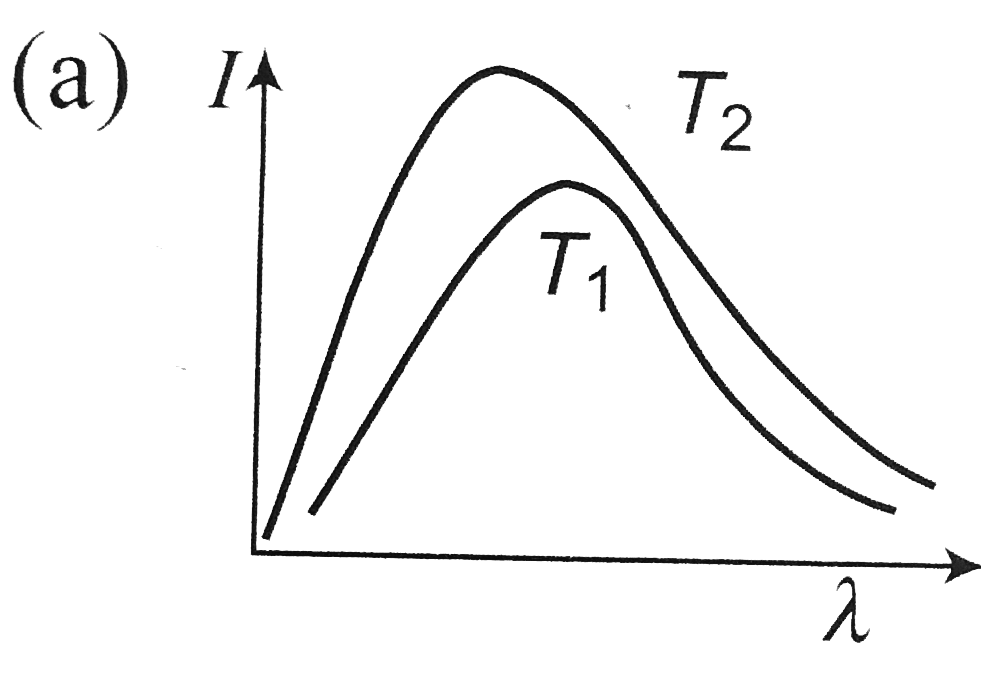
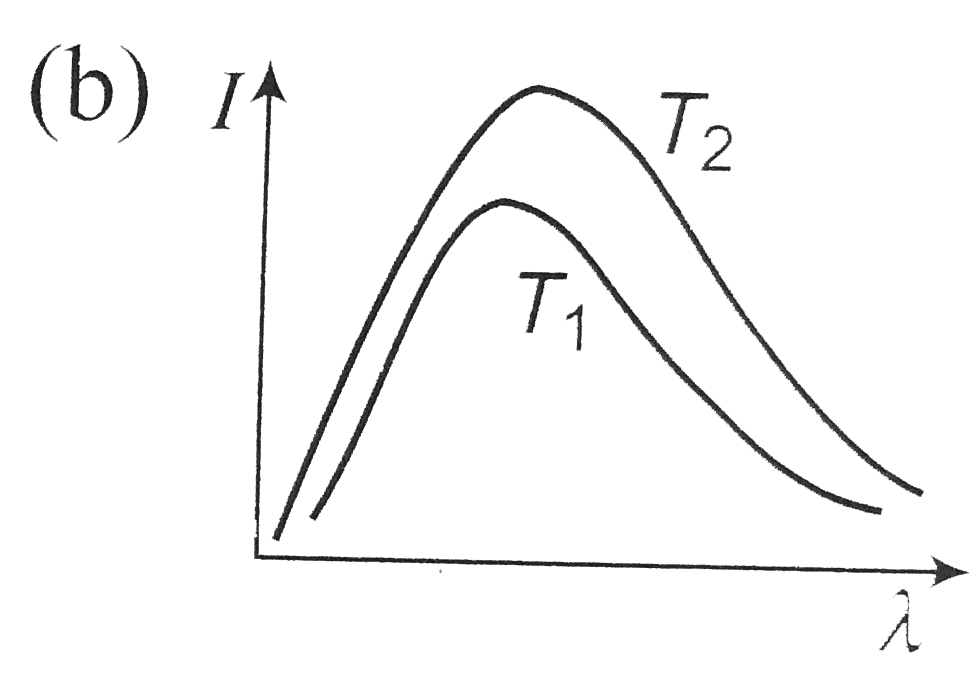
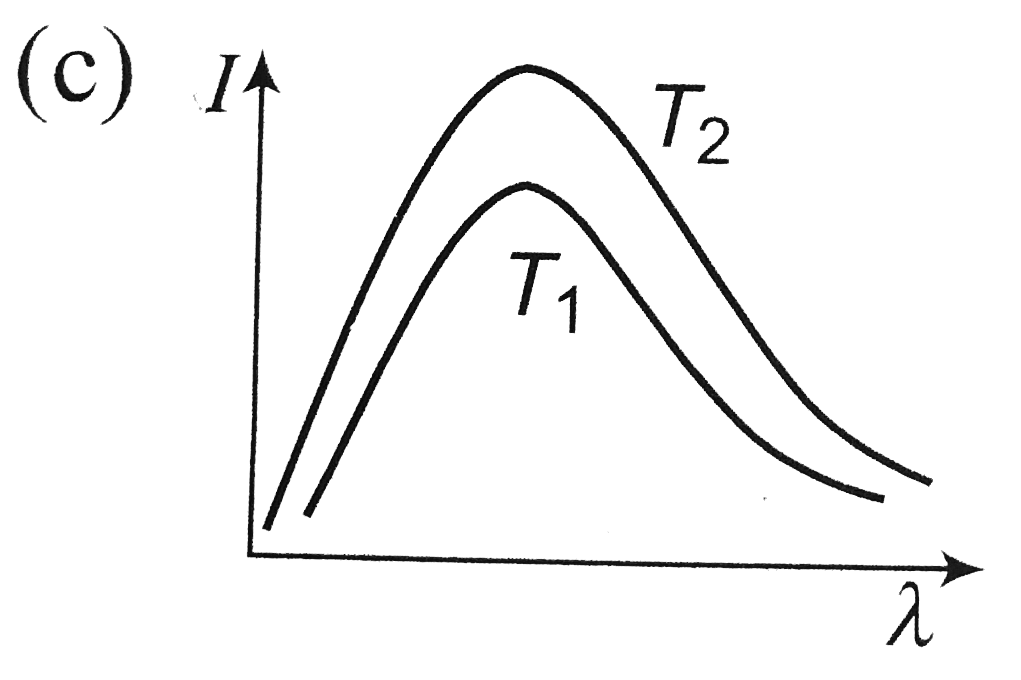
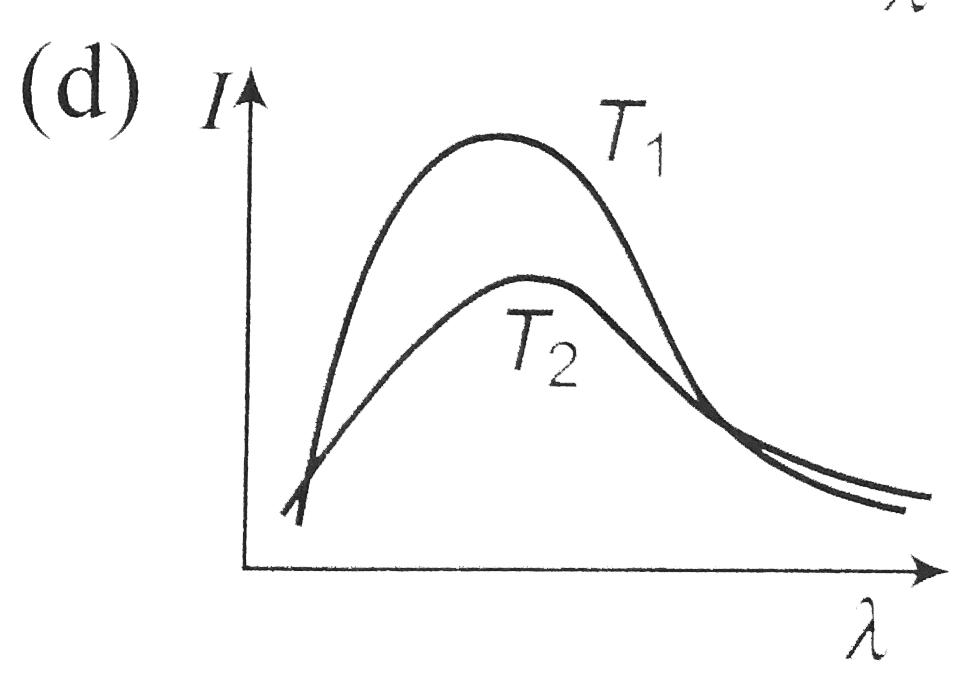
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
THERMAL PROPERTIES OF MATTER
A2Z|Exercise Chapter Test|30 VideosView PlaylistTHERMAL PROPERTIES OF MATTER
A2Z|Exercise NEET Questions|47 VideosView PlaylistROTATIONAL DYNAMICS
A2Z|Exercise Chapter Test|29 VideosView PlaylistUNIT, DIMENSION AND ERROR ANALYSIS
A2Z|Exercise Chapter Test|28 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
A2Z-THERMAL PROPERTIES OF MATTER-AIIMS Questions
- The density of a substance at 0^(@)C is 10 g//c c and at 100^(@)C, its...
02:48
|
Play - A black body at a temperature of 227^(@)C radiates heat at a rate of 2...
02:33
|
Play - Shown below are the black body radiation curves at temperature T(1) an...
02:38
|
Playing Now - Suppose the sun expands so that its radius becomes 100 times its prese...
02:13
|
Play - Three objects coloured black, gray and white can withstand hostile con...
01:52
|
Play - A bimetallic strip consists of metals X and Y, it is mounted rigidly a...
01:18
|
Play - A brass disc fits snugly in a hole in a steel plate. Should you heat o...
01:42
|
Play - On heating a liquid of coefficient of cubical expansion gamma in a con...
02:05
|
Play - The coefficient of thermal conductivity of copper, mercury and glass a...
02:17
|
Play - The initial temperature of a body is 80^(@)C. If its temperature falls...
04:01
|
Play - At 1 atmospheric pressure, 1.000 g of water having a volume of 1.000 ...
02:35
|
Play - Assertion : Woolen clothes keep the body warm in winter Reason : Air...
01:13
|
Play - Assertion : Blue star is at high temperature than red star. Reason :...
01:55
|
Play - Assertion : Temperature near the sea-coast are moderate. Reason : Wa...
01:20
|
Play - Assertion : It is hotter over the top of a fire than at the same dista...
01:37
|
Play - Assertion : The melting point of ice decreases with increase of pressu...
03:50
|
Play - Assertion : A body that is a good radiator is also a good absorber of ...
01:20
|
Play - Assertion : For higher temperature, the peak emission wavelength of a ...
01:23
|
Play - Assertion : Perspiration from human body helps in cooling the body. ...
01:11
|
Play - Assertion : The equivalent thermal conductivity of two plates of same ...
03:53
|
Play