Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
PRADEEP-THE HUMAN EYE AND COLOURFUL WORLD-(Mock Test)Sec - B
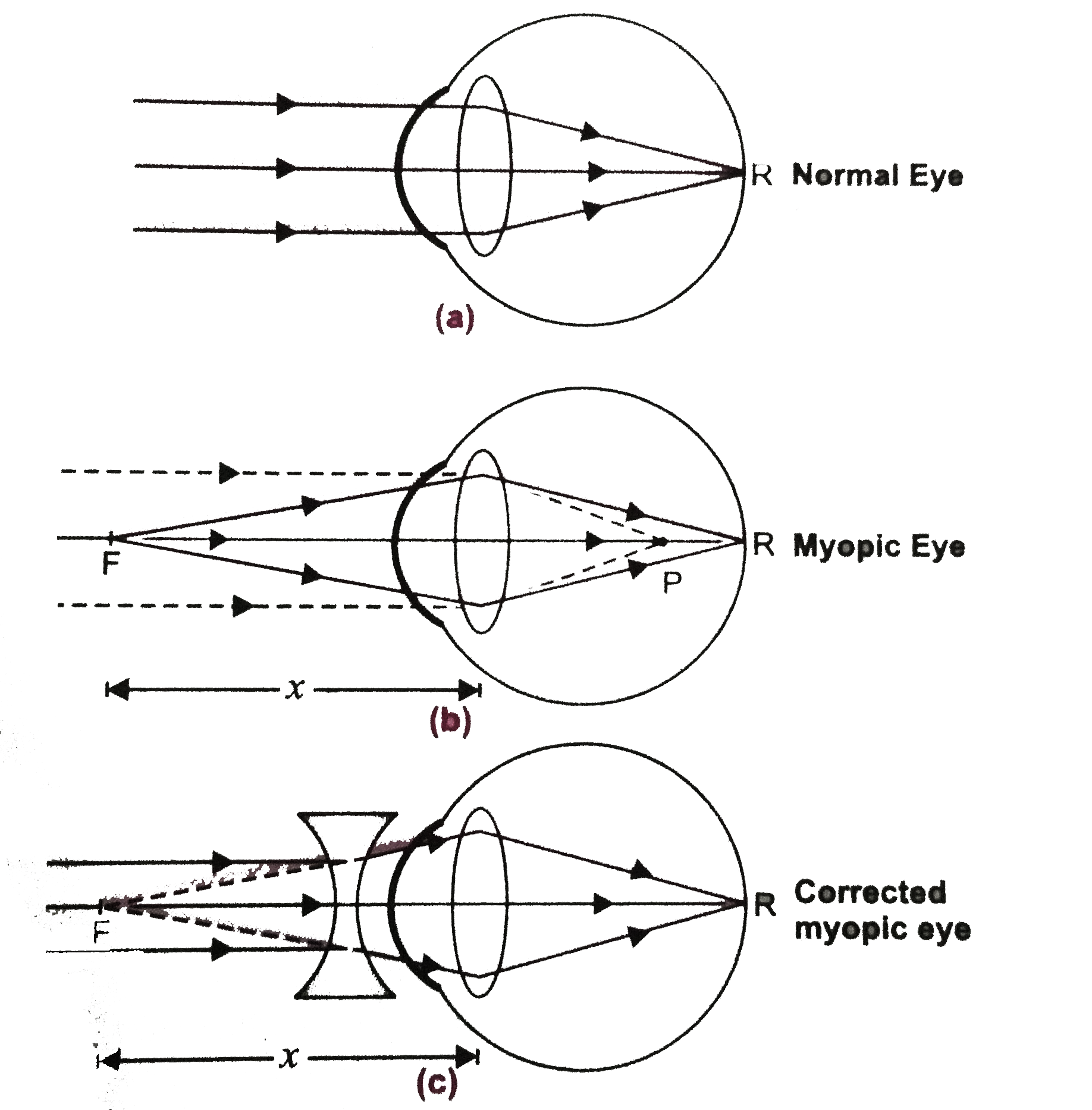
- (a) A student suffering from myopia is not able to see distinctly the ...
Text Solution
|
- On what factors does of deviation produced by a prism depend ?
Text Solution
|
- A ray of light falls on one face of an equilateral prism at an angle o...
Text Solution
|
- A ray of light is incident on one face of prism making an angle of 50^...
Text Solution
|
- In the minimum deviation position of a prism how are angle of incidenc...
Text Solution
|
- In the minimum deviation position of an equilateral prism, angle of de...
Text Solution
|
- A narrow beam of white light is shown to pass through a triangular gla...
Text Solution
|
 .
.