Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
LAWS OF MOTION
PRADEEP|Exercise JEE (Main and Advanced)/ Medical Entrance Special|93 VideosView PlaylistLAWS OF MOTION
PRADEEP|Exercise Integer Type Questions|7 VideosView PlaylistLAWS OF MOTION
PRADEEP|Exercise Fill in the blanks|20 VideosView PlaylistKINEMATICS
PRADEEP|Exercise 1 NCERT Comprehension|4 VideosView PlaylistMATHEMATICAL TOOLS
PRADEEP|Exercise Fill in the blanks|5 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
PRADEEP-LAWS OF MOTION-Problems for practice
- Two bodies whose masses are m(1) =50kg and m(2) =150kg are tied by a ...
02:36
|
Play - Two blocks of mass m(1) and m(2) lie on smooth horizontal table in co...
01:43
|
Play - When we ignore friction and mass of pulley what would be the accelerat...
03:47
|
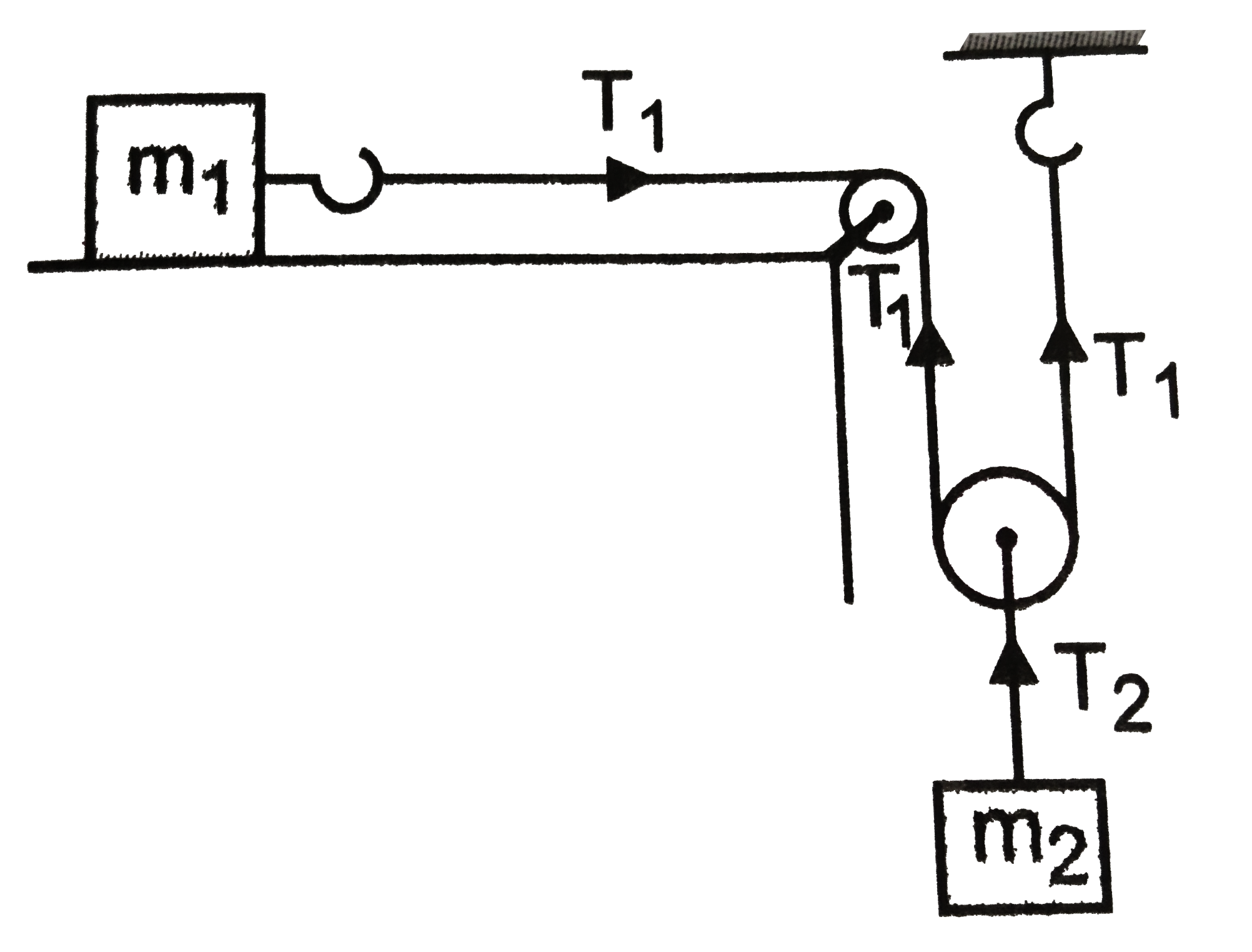
Playing Now - In the arrangement shown in show that tension in the string between ma...
06:07
|
Play - A car of mass one metric ton travelling at 32m//sc dashes into the rea...
02:49
|
Play - The force on a particle of mass 10g is (hati 10+hatj 5)N If it starts ...
04:12
|
Play - A suitcase is gently dropped on a conveyor belt moving at 3ms^(-1) If ...
03:19
|
Play - An engine of 100H.P draws a train of mass 100 metic ton with a velocit...
04:35
|
Play - A force ofv 3kg wt is just sufficient to pull a block of 4kg over a ho...
03:37
|
Play - An automobile is moving on a horizontal road with a speed upsilon If t...
02:22
|
Play - A motor car running at the rate of 7ms^(1) can be stooped by applying ...
01:55
|
Play - A horizontal force of 1.2kg is applied on a 1.5kg block, which rests o...
02:40
|
Play - A car starts with a velocity of 100m//s on a half kilometre long bridg...
05:29
|
Play - A train weighing 1000 quintals is running on a level road with a unifr...
02:29
|
Play - A body moving on the ground with a velocity of 15m//s comes to rest af...
03:06
|
Play - A box of mass 4kg rests upon an inclined plane This inclination is gra...
05:47
|
Play - When a car moving with a speed of 36km//h reaches an upwards inclined ...
03:14
|
Play - An engine of mass 6.5 metric ton is going up an incline of 5 in 13 at...
04:20
|
Play - A body of mass m is released from the top of a rough inclined plane of...
03:03
|
Play - A block slides down an incline of 30^(@) with the horizontal starting...
06:13
|
Play
 .
.