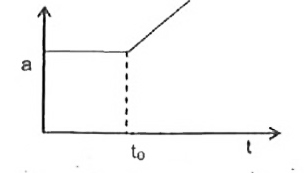
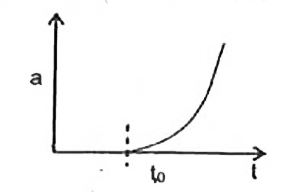
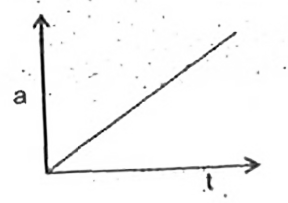
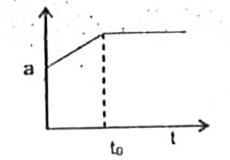
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
LAWS OF MOTION
PRADEEP|Exercise Integer Type Questions|7 VideosView PlaylistLAWS OF MOTION
PRADEEP|Exercise Assertion- Reason Type Questions|17 VideosView PlaylistLAWS OF MOTION
PRADEEP|Exercise Problems for practice|112 VideosView PlaylistKINEMATICS
PRADEEP|Exercise 1 NCERT Comprehension|4 VideosView PlaylistMATHEMATICAL TOOLS
PRADEEP|Exercise Fill in the blanks|5 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
PRADEEP-LAWS OF MOTION-JEE (Main and Advanced)/ Medical Entrance Special
- A block of mass is placed on a surface with a vertical cross section g...
02:21
|
Play - A uniform wooden stick of mass 1.6 kg and length l rests in an incline...
05:23
|
Play - A block of mass 4kg is placed on a rough horizontal plane A time depen...
01:54
|
Playing Now - A block is gently placed on a conveyor belt moving horizontal with con...
02:41
|
Play - A 30kg block rests on a rough horizontal surface A force of 200N is ap...
02:48
|
Play - A wooden box of mass 8kg slides down an inclined plane of inclination ...
02:22
|
Play - The upper half of an inclined plane with inclination phi is perfectly ...
05:20
|
Play - A body takes time t to reach the bottom of a smooth inclined plane of ...
05:27
|
Play - A given object taken n time more time to slide down 45^(@) rough incli...
04:04
|
Play - The coefficient of static friction mu(s) between block A of mass 2kg a...
01:41
|
Play - The rear side of a truck is open and a box of mass 20kg is placed on t...
03:45
|
Play - A parabolic bow1 with its bottom at origin has the shape y = (x^(2))/(...
02:28
|
Play - A block of mass m is on an inclined plane of angle theta. The coeffici...
07:07
|
Play - A block of mass m is in contact with the cart C as shown in The coeffi...
02:30
|
Play - A block is moving on an inclined plane making an angle 45^@ with the h...
07:31
|
Play - A mas m hangs with help of a string wraped around a pulley on a fricti...
02:09
|
Play - An insect craws up a hemispherical surface very slowly (see fig.). The...
05:03
|
Play - A system consists of three masses m(1) , m(1) , m(1) , m(2) and m(3) c...
05:44
|
Play - A block of mass is placed on a surface with a vertical cross section g...
02:21
|
Play - What is the minimum velocity with which a body of mass m must enter a...
01:32
|
Play