A
B
C
D
Text Solution
Verified by Experts
|
Topper's Solved these Questions
NUCLEAR PHYSICS
RESONANCE|Exercise Advanced level solutions|16 VideosView PlaylistSEMICONDUCTORS
RESONANCE|Exercise Exercise 3|88 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
RESONANCE-REVISION DPP-All Questions
- Sand is falling on a flat car being pulled with constant speed. The ra...
02:06
|
Play - A particle is moving along an elliptical path with constant speed. As ...
01:58
|
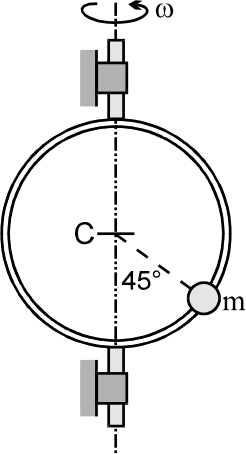
Play - A small bead of mass m = 1 kg is free to move on a circular hoop. The ...
04:37
|
Playing Now - Two blocks of mass m(1) and m(2) (m(1) lt m(2)) are connected with an ...
04:36
|
Play - Three point masses are attached by light inextensible strings of vario...
02:45
|
Play - One end of a light rod of length 1m is attached with a string of lengt...
01:33
|
Play - Particle sticks to wooden loop, If particle reach at the lowest positi...
02:00
|
Play - Two identical blocks A and B of mass m each are connected to each othe...
04:04
|
Play - Three identical particles A, B and C of mass m lie on a smooth horizo...
09:02
|
Play - A particle is attached to an end of a rigid rod. The other end of the ...
02:12
|
Play - A particle is moving in a uniform circular motion on a horizontal surf...
02:26
|
Play - The linear momentum of a particle is given by vec(P)=(a sin t hati- ac...
05:52
|
Play - A circular road of radius r is banked for a speed v=40 km/hr. A car of...
05:48
|
Play - A cylinder of radius R is rotating about its horizontal axis with cons...
04:21
|
Play - A gun which fires small balls of mass 20 g is firing 20 balls per seco...
07:18
|
Play - A rocket of total mass 1000kg initially is launched from ground. The g...
02:18
|
Play - AB is a long frictionless horizontal surface. One end of an ideal spri...
01:13
|
Play - In a region, potential energy varies with X as U(x)=30-(x-5)^(2) Joule...
11:33
|
Play - Two particles A and B are revolving with constant angular velocity on ...
01:23
|
Play - Work done by force F to move block of mass 2 kg from A to C very slowl...
07:42
|
Play