Home
Class 10
MATHS
Which theorem do we use in proving that ...

Which theorem do we use in proving that hypotenuse is the longest side of a right angled traingle?

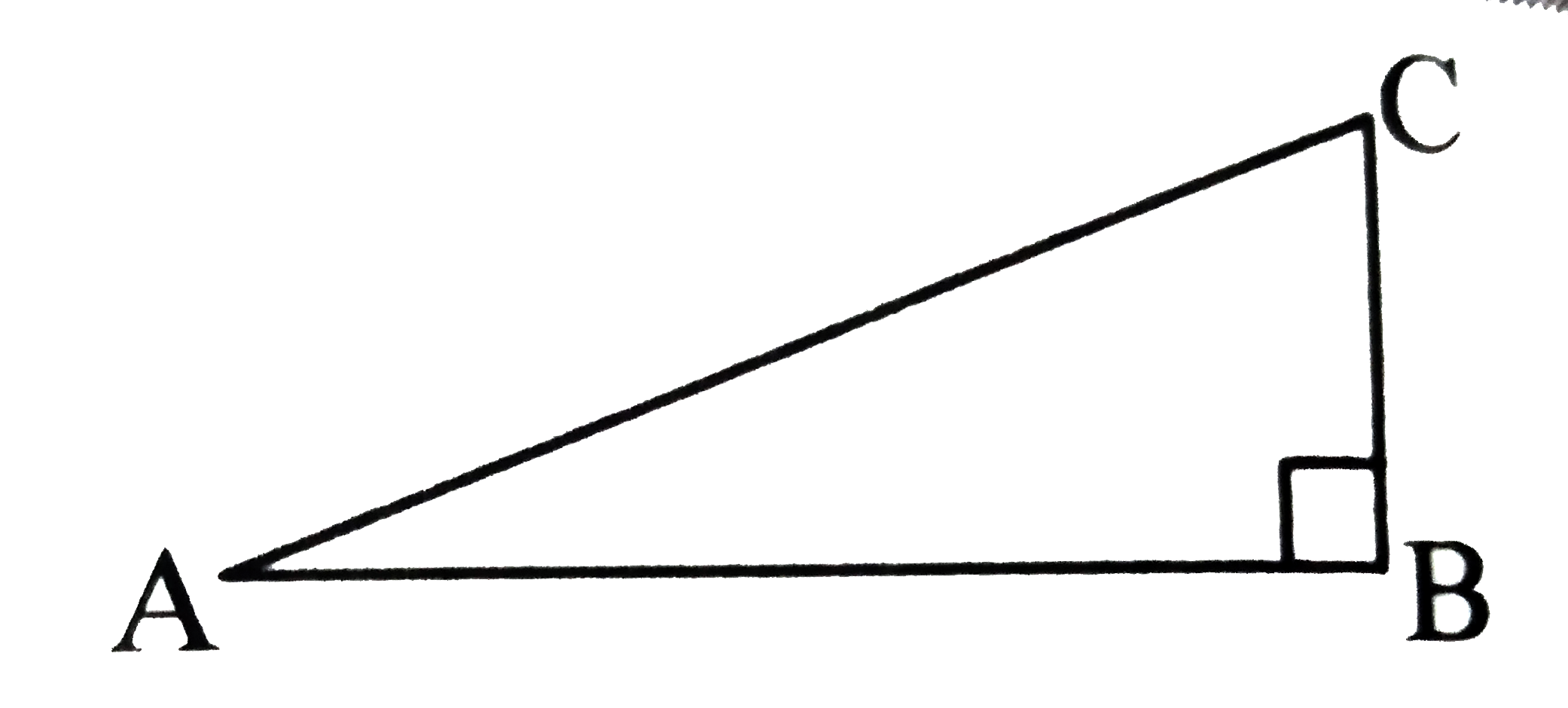
Text Solution

Verified by Experts

The correct Answer is:
`therefore`Hypotenuse is the longest side in right angled traingle.
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • CIRCLE

    TARGET PUBLICATION|Exercise Try this|8 Videos

  • CIRCLE

    TARGET PUBLICATION|Exercise Practice Set 3.1|4 Videos

  • CIRCLE

    TARGET PUBLICATION|Exercise Textual Activities|9 Videos

  • CHALLENGING QUESTIONS

    TARGET PUBLICATION|Exercise Chapter 6: Statistics|4 Videos

  • CO-ORDINATE GEOMETRY

    TARGET PUBLICATION|Exercise CHAPTER ASSESSMENT|19 Videos

Similar Questions

Explore conceptually related problems

1. Show that the hypotenuse is the longest side in the right angled triangle. it occurs.

Show that in a right angled triangle, the hypotenuse is the longest side.

Knowledge Check

  • If the sum of lengths of the hypotenuse and another side of a right angled triangle is given, show that the area of the triangle is max. when, the angle between these is

    A
    `pi/12`
    B
    `pi/4`
    C
    `pi/3`
    D
    `pi/2`

    • Similar Questions

    Explore conceptually related problems

    Show that in a right triangle the hypotenuse is the longest side.GIVEN : A right triangle ABC in which /_ABC=90^(@). TO PROVE : Hypotenuse AC is the longest side,i.e.AC>AB( ii) AC>BC

    Show that in a right angled triangle,the hypotenuse is the longest side.

    Identify the shapes on the basis of description. (i) A three-sided polygon with all sides equal (ii) The longest side of a right-angled triangle.

    If the sum of the lengths of the hypotenuse and another side of a right-angled triangle is given,show that the area of the triangle is maximum when the angle between these sides is (pi)/(3).

    Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.

    Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle

    In a triangle, if the square on one side is equal to the sum of the squares on the other two sides, prove that the angle opposite to the first side is a right angle. Use the above theorem to find the measure of anglePKR in Fig. 7.52.

    Home
    Profile