A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
ATOMIC STRUCTURE
P BAHADUR|Exercise Exercise 3B|19 VideosView PlaylistATOMIC STRUCTURE
P BAHADUR|Exercise Exercise 4|39 VideosView PlaylistATOMIC STRUCTURE
P BAHADUR|Exercise Exercise|19 VideosView PlaylistCHEMICAL BONDING
P BAHADUR|Exercise Exercise 7|11 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
P BAHADUR-ATOMIC STRUCTURE-Exercise 3A
- Which of the following is correct for the same radius of ion ieach pai...
01:54
|
Play - IE1 for .1H^2 and IE1 for .1H^1 are related as ?
01:42
|
Play - The spein multipltcity for the orbital enryron si 2s +1where (s) is t...
01:55
|
Playing Now - The enrgy level fo 4s-orbital is less than 3d- orbital because :
02:17
|
Play - The number fo spectiral lines produced according to Bohr's concept whe...
01:13
|
Play - A s-orbital is symmetricla aout the :
01:23
|
Play - Which orbital has appearance like a body soother ?
01:45
|
Play - Degenrate orbitals means :
01:23
|
Play - Which is correct paramagnetic or der ?
02:12
|
Play - In ground state fo .(24)Cr :
03:44
|
Play - The maxium number of electrons in an orbital having same spin quantum ...
02:57
|
Play - The electronic configuration of .(46)Pd is :
01:40
|
Play - The pair having identical velue fo e//m:
01:35
|
Play - For an electron the product of velocity fo electron and pricipa quantu...
01:29
|
Play - Which of the following corresponds to one node ?
Text Solution
|
Play - For a satellite moving in an orbit aroun the earth the ratio of kineti...
01:18
|
Play - A photosensitve metallic surface has work fuction hv0 If photons of ...
03:29
|
Play - The work functions for metals A, B and ( C) are presepctively 1. 92 ...
02:33
|
Play - Carbo , silicon and Germanitum atomshave four valence electrons each ....
02:44
|
Play - The total enrgy of electron in the firdt state fo H-atom is -3 . 4 eV...
01:45
|
Play
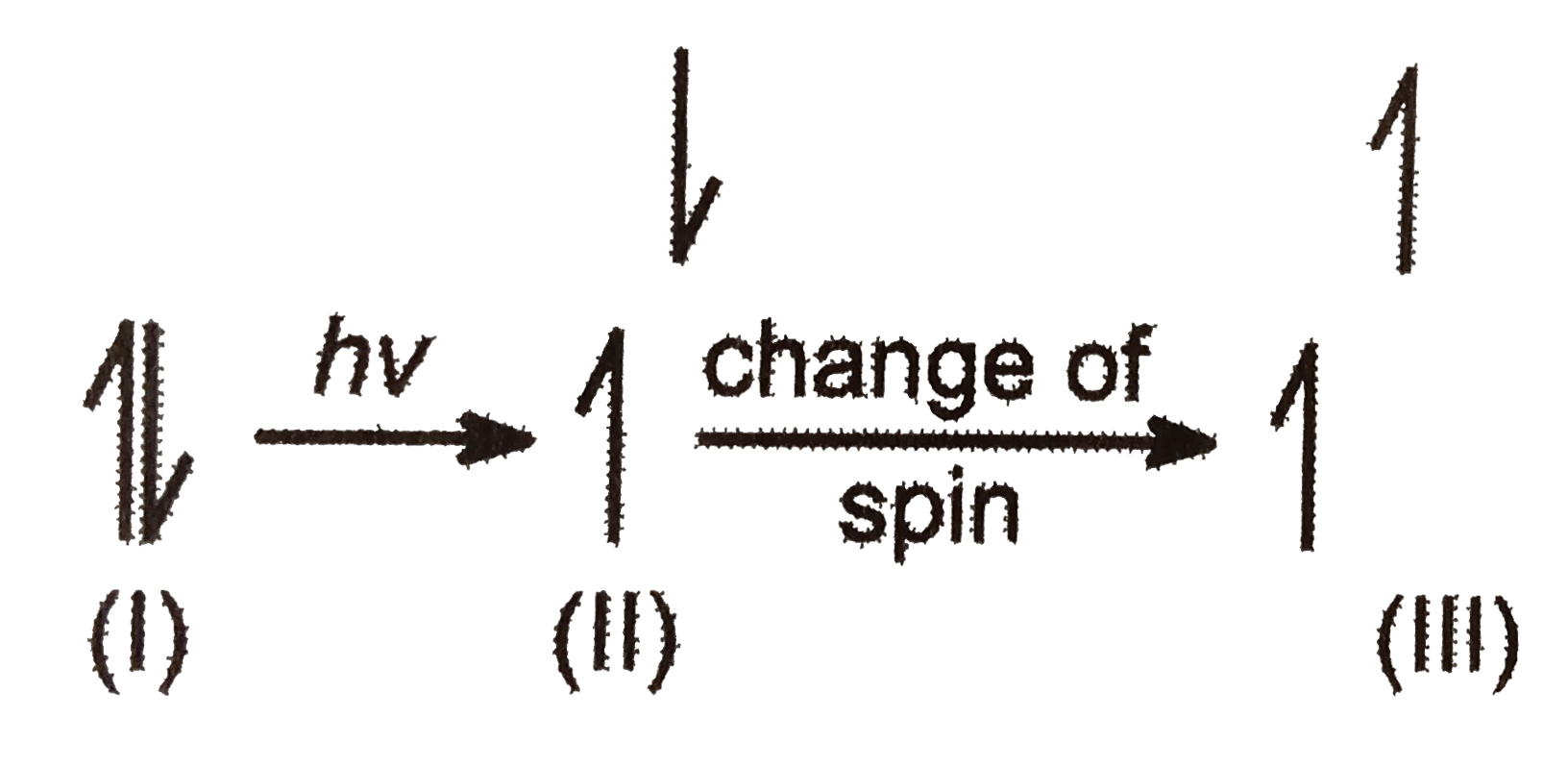 .
.