Home
Class 12
PHYSICS
Two small circular loops, marked (1) and...

Two small circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in figure. Find the magnitude and direction of the net magnetic field produced at the point O.

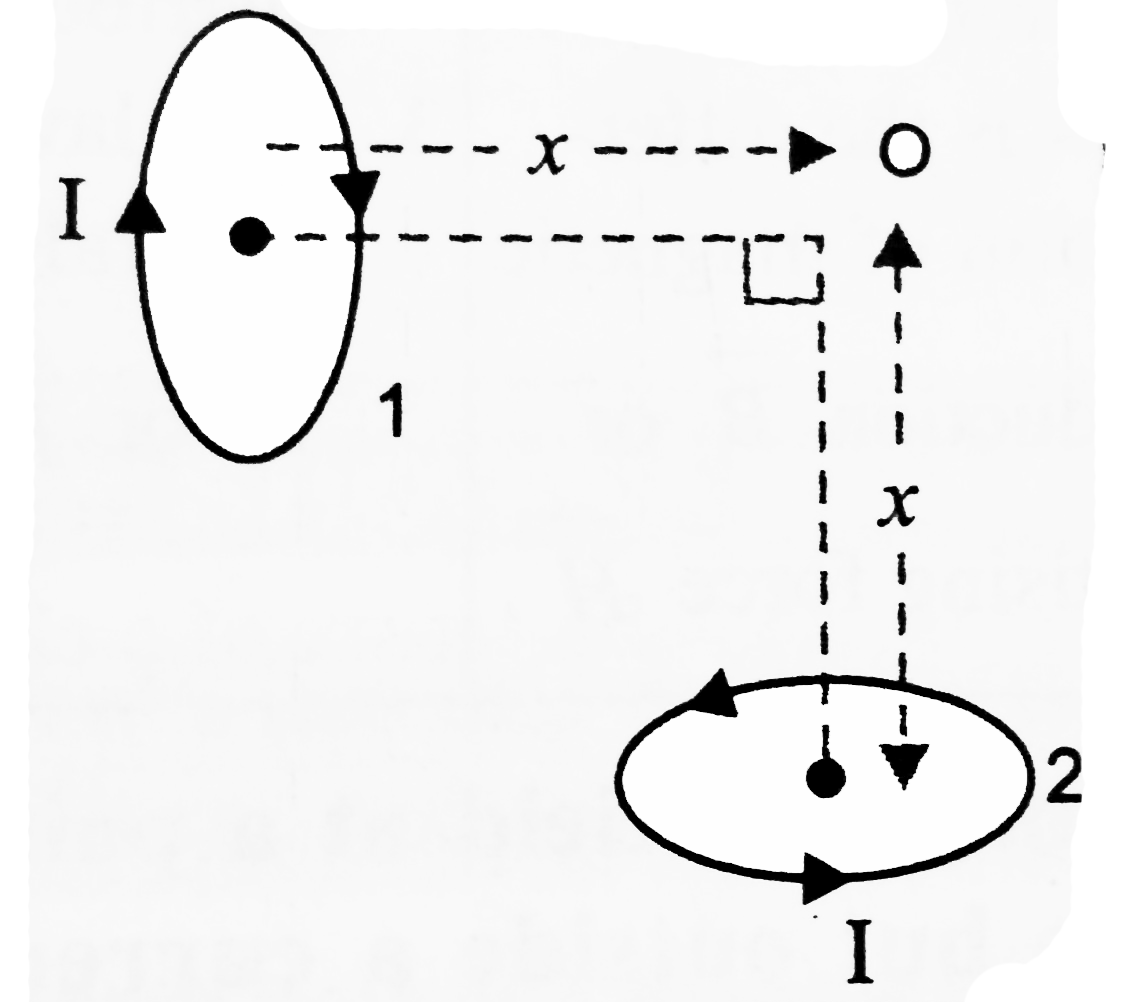
Text Solution

Verified by Experts

Magnetic field induction at O due to current loop 1 is
`B_1=(mu_0IR^2)/(2(x^2+R^2)^(3//2))`,
acting towards left.
Magnetic field induction at O due to current loop 2 is
`B_2=(mu_0IR^2)/(2(x^2+R^2)^(3//2))`
acting vertically upwards.
Resultant magnetic field induction at O will be
`B=sqrt(B_1^2+B_2^2)=sqrt2B_1` (`:' B_1=B_2`)
`=sqrt2xx(mu_0IR^2)/(2(x^2+R^2)^(3//2))`
`=(mu_0IR^2)/(sqrt(x^2+R^2)^(3//2))`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • MAGNETIC EFFECT OF CURRENT AND MAGNETISM

    PRADEEP|Exercise Conceptual Problems (d)|2 Videos

  • MAGNETIC EFFECT OF CURRENT AND MAGNETISM

    PRADEEP|Exercise Very Short Answer Questions (a)|2 Videos

  • ELECTROSTATICS

    PRADEEP|Exercise ASSERTION-REASON TYPE QUESTIONS|2 Videos

  • OPTICS

    PRADEEP|Exercise Multiple choice questions|1 Videos

Similar Questions

Explore conceptually related problems

Two small identical circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in the fig. Find the fig. Find the magnitude and direction of the net magnetic field at the net magnetic field at the point O.

(a) Using Biot-Savart's law, derive an expression for the magnetic field at the centre of a circular coil of radius R, number of turns N, carrying current. (b) Two small identical circular coils marked 1,2 carry equal currents and are placed with their geometric axes perpendicular to each other as shown in the figure. Derive an expression for the resultant magnetic field at O.

Knowledge Check

  • A current - carrying loop is shown in the figure. The magnitude of the magnetic field produced at a point O is

    A
    `(mu_(0)I)/(4R)`
    B
    `(mu_(0)I)/(2R)(1+(sqrt2)/(pi))`
    C
    `(mu_(0)I)/(4R)(1+(sqrt2)/(pi))`
    D
    `(mu_(0))/(4R)(1+(2sqrt2)/(pi))`

    • Similar Questions

    Explore conceptually related problems

    Two identical circular loops P and Q carrying equal currents are placed such that their geometrical axis are perpendicular to each other as shown in figure. And the direction of current appear’s anticlockwise as seen from point O which is equidistant from loop P and Q. Find the magnitude and direction of the net magnetic field produced at the p oint O. tan theta = (B_2)/(B_1)=1, theta = pi//4 .

    There are two parallel current carrying wires X and Y as shown in figure. Find the magnitude and direction of the magnetic field at points, P, Q and R.

    Two identical circular coils, P and Q, carrying currents 1A and sqrt3A respectively, are placed concentrically and perpendicular to each other lying in the XY and YZ plane. Find the magnitude and direction of the net magnetic field at the centre of the coils.

    Two identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.

    Two identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in fig. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.

    Two parallel coaxial circular coils of equal radius R and equal number of turns N carry equal currents I in the same direction and are separated by a distance 2R . Find the magnitude and direction of the net magnetic field produced at the mid-point of the line joining their centres.

    Two identical circular coils, P and Q each of radius R, carrying currents 1 A and sqrt(3) A respectively, are placed concentrically are perpendicualr to each other lying in the XY and YZ planes. Find the magnitude and direction of the net magnetic field at the centre of the coils.

    Home
    Profile