Light guidance in an optical fibre can be understood by considering a structure comprising of thin solid glass cylinder of refractive index `n_1` surrounded by a medium of lower refractive index `n_2`. The light guidance in the structure takes place due to successive total internal reflectrions at the interface of the media `n_1` and `n_2` as shown in the fugure. All rays with the angle of incidence i less than a particular value `i_m` are confined in the medium of refractive index `n_1`. The numerical aprture (NA) of the structure is defined as `sini_m`
If two structure of same cross-sectional area, but different numerical apertures `NA_1`and `NA_2(NA_2ltNA_1)` are joined longitudinally, the numerical aperture of the combined structure is `
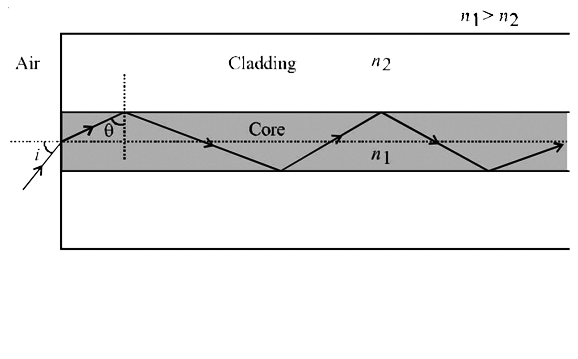
Light guidance in an optical fibre can be understood by considering a structure comprising of thin solid glass cylinder of refractive index `n_1` surrounded by a medium of lower refractive index `n_2`. The light guidance in the structure takes place due to successive total internal reflectrions at the interface of the media `n_1` and `n_2` as shown in the fugure. All rays with the angle of incidence i less than a particular value `i_m` are confined in the medium of refractive index `n_1`. The numerical aprture (NA) of the structure is defined as `sini_m`
If two structure of same cross-sectional area, but different numerical apertures `NA_1`and `NA_2(NA_2ltNA_1)` are joined longitudinally, the numerical aperture of the combined structure is `

If two structure of same cross-sectional area, but different numerical apertures `NA_1`and `NA_2(NA_2ltNA_1)` are joined longitudinally, the numerical aperture of the combined structure is `

A
`NA` of `S_(1)` immersed in water is same as that of `S_(2)` immersed in a liquid of refractive index `(16)/(3sqrt(15))`,
B
`NA` of `S_(1)` immersed in liquid of refractive index `(6)/(sqrt(15))` is the same as that of `S_(2)` immersed in water.
C
`NA` of `S_(1)` placed in air same as that of `S_(2)` immersed in liquid of refracitve index `(4)/(sqrt(15))`
D
`NA` of `S_(1)` placed in air is the same as that of `S_(2)` placed in water.
Text Solution
Verified by Experts
The correct Answer is:
A, C
Here, `n_(s) rarr` refractive index of surrounding medium
As `n_(s) sin i_(m) = n_(1) sin(90^(@) - C)` …(i)
Also, `sin C = (1)/(mu) = (n_(2))/(n_(1))` …(ii)
As `NA = sin i_(m)`
From (i), `sin i_(m) = (n_(1))/(n_(s)) sin (90^(@) - C)`
`= (n_(1))/(n_(s)) cos C = (n_(1))/(n_(s)) sqrt(1 - sin^(2) C)`
`:. NA = (n_(1))/(n_(s))sqrt(1 - (n_(2)^(2))/(n_(1)^(2))) = (1)/(n_(s))sqrt(n_(1)^(2) - n_(2)^(2))`
[from (ii)]
For `S_(1)` in air, `n_(s) = 1, n_(1) = (sqrt(45))/(4), n_(1) = (3)/(2)`
`NA = (1)/(1) = sqrt((45)/(16) - (9)/(4)) = (3)/(4)`
`NA = (sqrt(15))/(6)sqrt((45)/(16) - (9)/(4)) = (3sqrt(15))/(24) = (sqrt(15))/(8)`
For `S_(1)` in water
`NA = (1)/(4//3)sqrt((45)/(16) - (9)/(4)) = (3)/(4)((3)/(4)) = (9)/(16)`
For `S_(2)` in air , `n_(s) = 1, n_(1) = (8)/(5), n_(2) = (7)/(5)`
`NA = (1)/(1)sqrt((64)/(25) - (49)/(25)) = (sqrt(15))/(5)`
For `S_(2)` in water, `n_(2) = (4)/(3)`
`NA = (1)/(4//3)sqrt((64)/(25) - (49)/(25)) = (3)/(4)(sqrt(15))/(5)`
For `S_(2)` in `n_(s) = (16)/(3sqrt(15))`
`NA = (3sqrt(15))/(16)sqrt((64)/(25) - (49)/(25)) = (9)/(16)`
For `S_(2)` in `n_(s) = (4)/(sqrt(15))`
`NA = (sqrt(15))/(4)sqrt((64)/(25) - (49)/(25)) = (3)/(4)`
Hence, options 'a' and 'c' are correct.
As `n_(s) sin i_(m) = n_(1) sin(90^(@) - C)` …(i)
Also, `sin C = (1)/(mu) = (n_(2))/(n_(1))` …(ii)
As `NA = sin i_(m)`
From (i), `sin i_(m) = (n_(1))/(n_(s)) sin (90^(@) - C)`
`= (n_(1))/(n_(s)) cos C = (n_(1))/(n_(s)) sqrt(1 - sin^(2) C)`
`:. NA = (n_(1))/(n_(s))sqrt(1 - (n_(2)^(2))/(n_(1)^(2))) = (1)/(n_(s))sqrt(n_(1)^(2) - n_(2)^(2))`
[from (ii)]
For `S_(1)` in air, `n_(s) = 1, n_(1) = (sqrt(45))/(4), n_(1) = (3)/(2)`
`NA = (1)/(1) = sqrt((45)/(16) - (9)/(4)) = (3)/(4)`
`NA = (sqrt(15))/(6)sqrt((45)/(16) - (9)/(4)) = (3sqrt(15))/(24) = (sqrt(15))/(8)`
For `S_(1)` in water
`NA = (1)/(4//3)sqrt((45)/(16) - (9)/(4)) = (3)/(4)((3)/(4)) = (9)/(16)`
For `S_(2)` in air , `n_(s) = 1, n_(1) = (8)/(5), n_(2) = (7)/(5)`
`NA = (1)/(1)sqrt((64)/(25) - (49)/(25)) = (sqrt(15))/(5)`
For `S_(2)` in water, `n_(2) = (4)/(3)`
`NA = (1)/(4//3)sqrt((64)/(25) - (49)/(25)) = (3)/(4)(sqrt(15))/(5)`
For `S_(2)` in `n_(s) = (16)/(3sqrt(15))`
`NA = (3sqrt(15))/(16)sqrt((64)/(25) - (49)/(25)) = (9)/(16)`
For `S_(2)` in `n_(s) = (4)/(sqrt(15))`
`NA = (sqrt(15))/(4)sqrt((64)/(25) - (49)/(25)) = (3)/(4)`
Hence, options 'a' and 'c' are correct.
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
Light guidance in an optical fibre can be understood by considering a structure comprising of thin solid glass cylinder of refractive index n_1 surrounded by a medium of lower refractive index n_2 . The light guidance in the structure takes place due to successive total internal reflectrions at the interface of the media n_1 and n_2 as shown in the fugure. All rays with the angle of incidence i less than a particular value i_m are confined in the medium of refractive index n_1 . The numerical aprture (NA) of the structure is defined as sini_m For two structure namely S_1 with n_1=(sqrt45)/(4) and n_2=(3)/(2) , and S_2 with n_1=(8)/(5) and n_2=(7)/(5) and taking the refractive index of water to be (4)/(3) and that of air to be 1, the correct option (s) is (are) ?
A glass slab made of a material of refractive index n_1 is kept in a medium of refractive index n_2 . A light ray is incident on the slab. Draw the path of the rays of light emerging from the glass slab, if n_1 lt n_2
A glass slab made of a material of refractive index n_1 is kept in a medium of refractive index n_2 . A light ray is incident on the slab. Draw the path of the rays of light emerging from the glass slab, if n_1 gt n_2
A glass slab made of a material of refractive index n_1 is kept in a medium of refractive index n_2 . A light ray is incident on the slab. Draw the path of the rays of light emerging from the glass slab, if n_1=n_2
Monochromatic light of wavelength lambda_1 travelling in medium of refractive index n_1 enters a denser medium of refractive index n_2 . The wavelength in the second medium is
A light ray moving in medium-I (of refractive index n_(1) ) is incident on interface of two media and it is totally internally reflected at the interface. Now, refractive index n_(2) of medium-II is decreased, then
The wavelength of light in vacuum is lambda . The wavelength of light in a medium of refractive index n will be