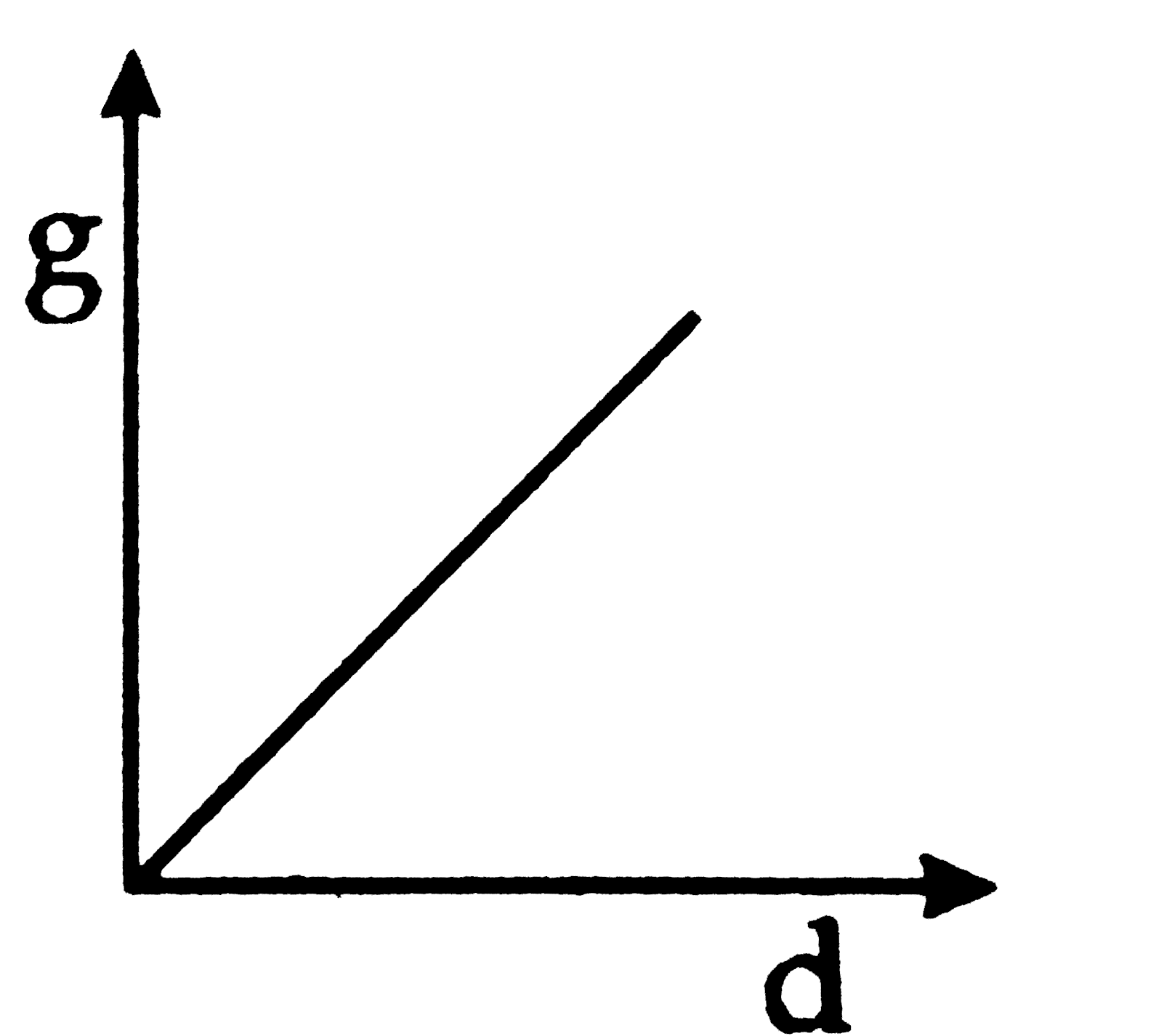
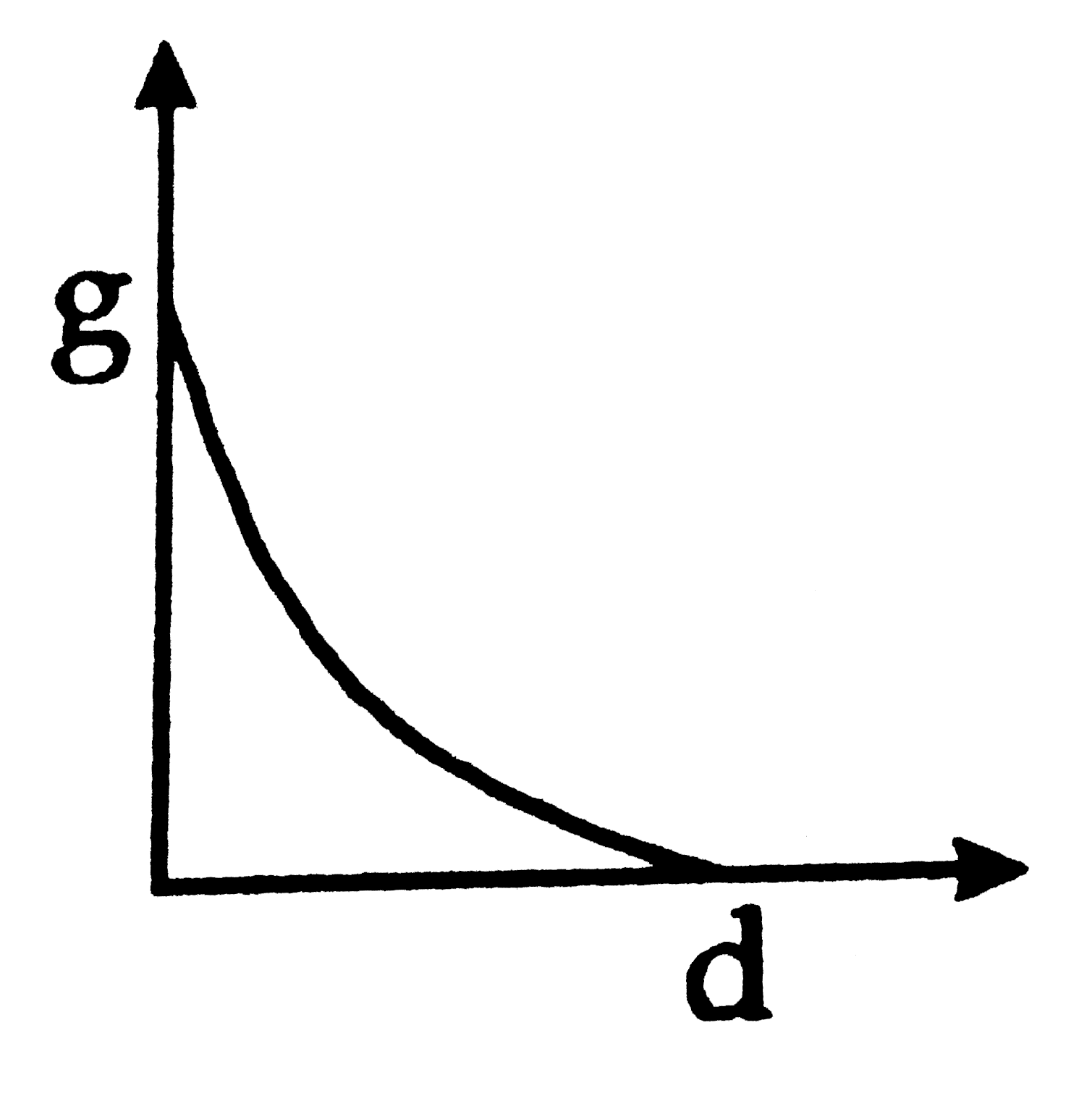
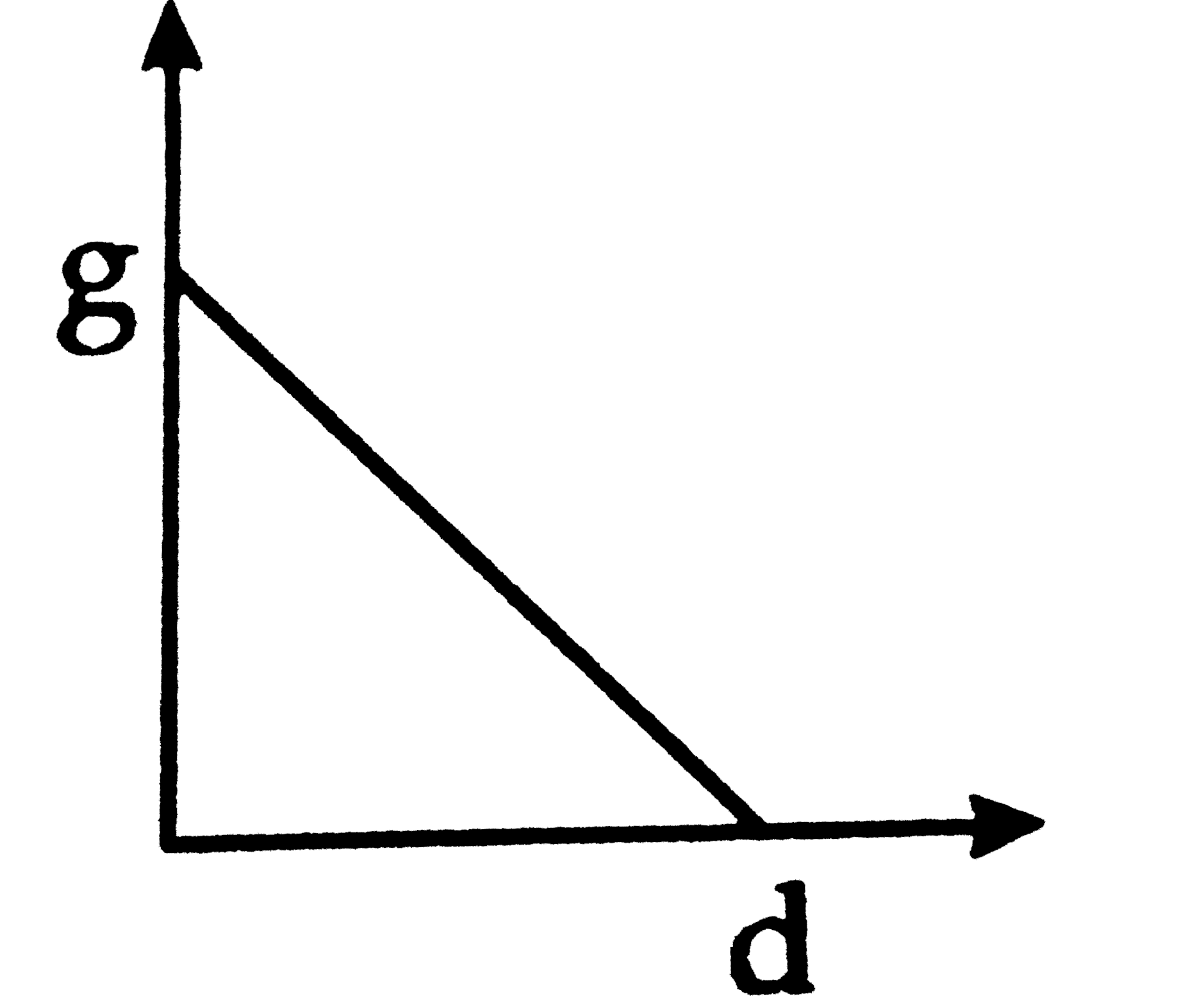
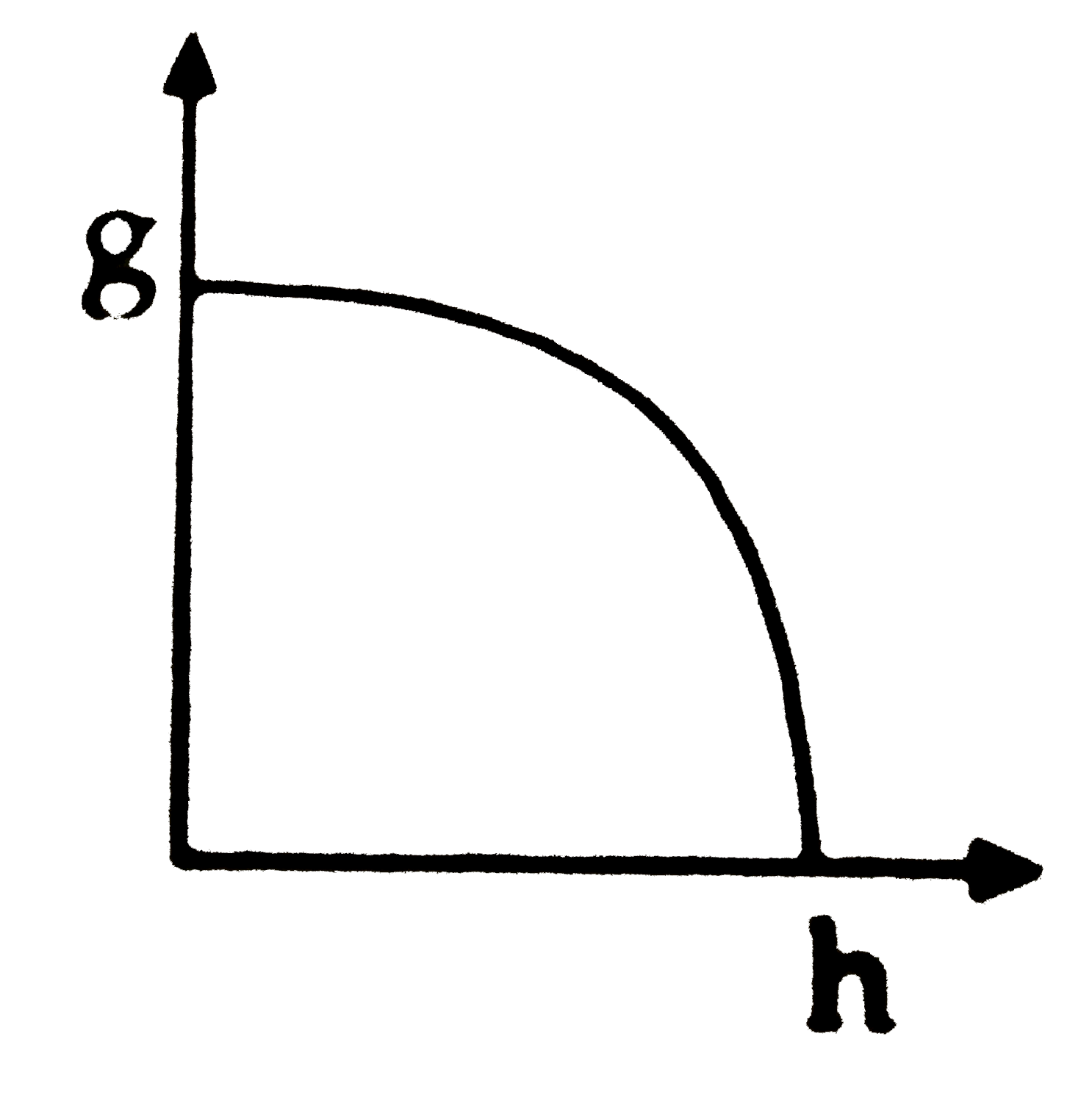
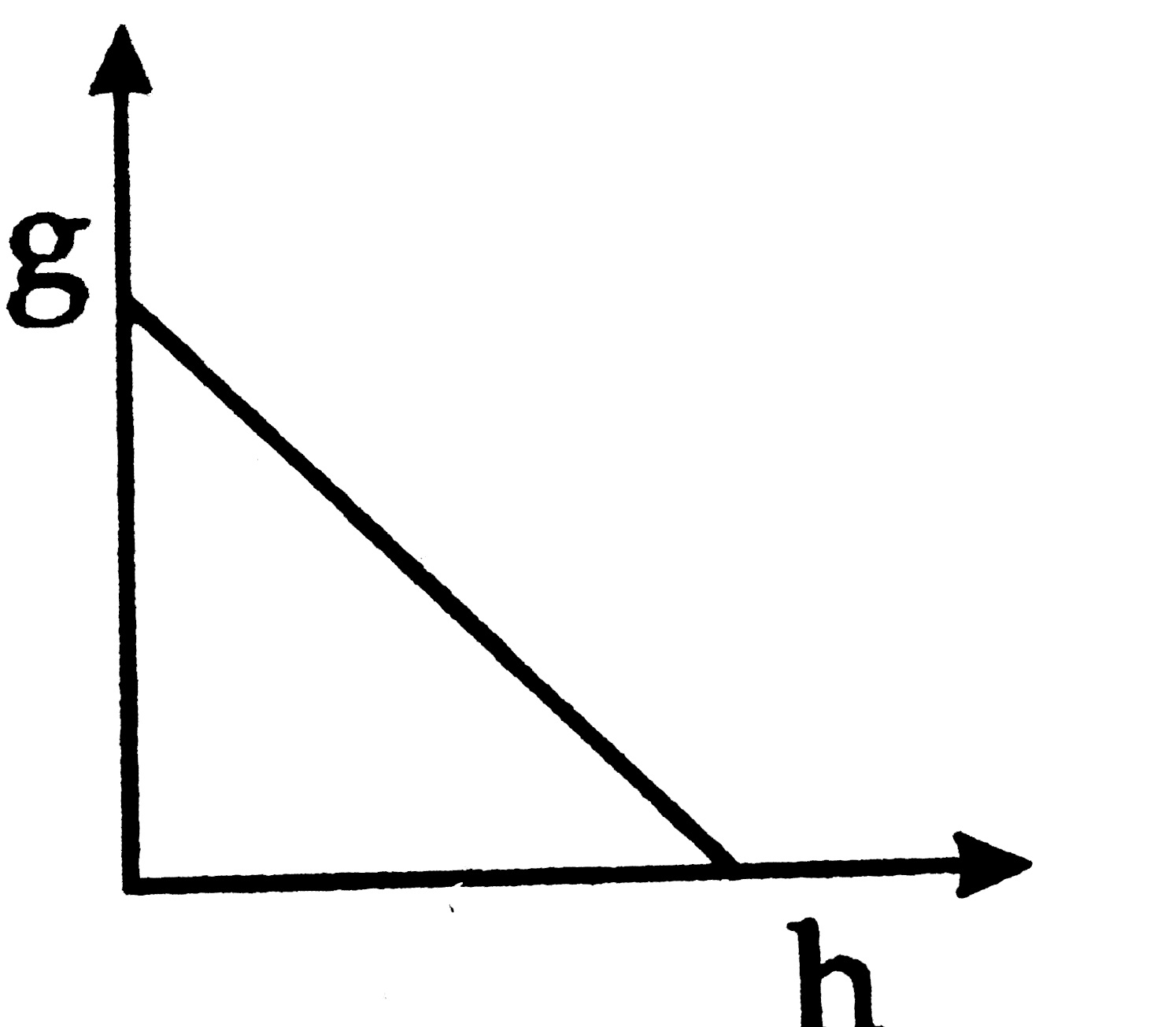
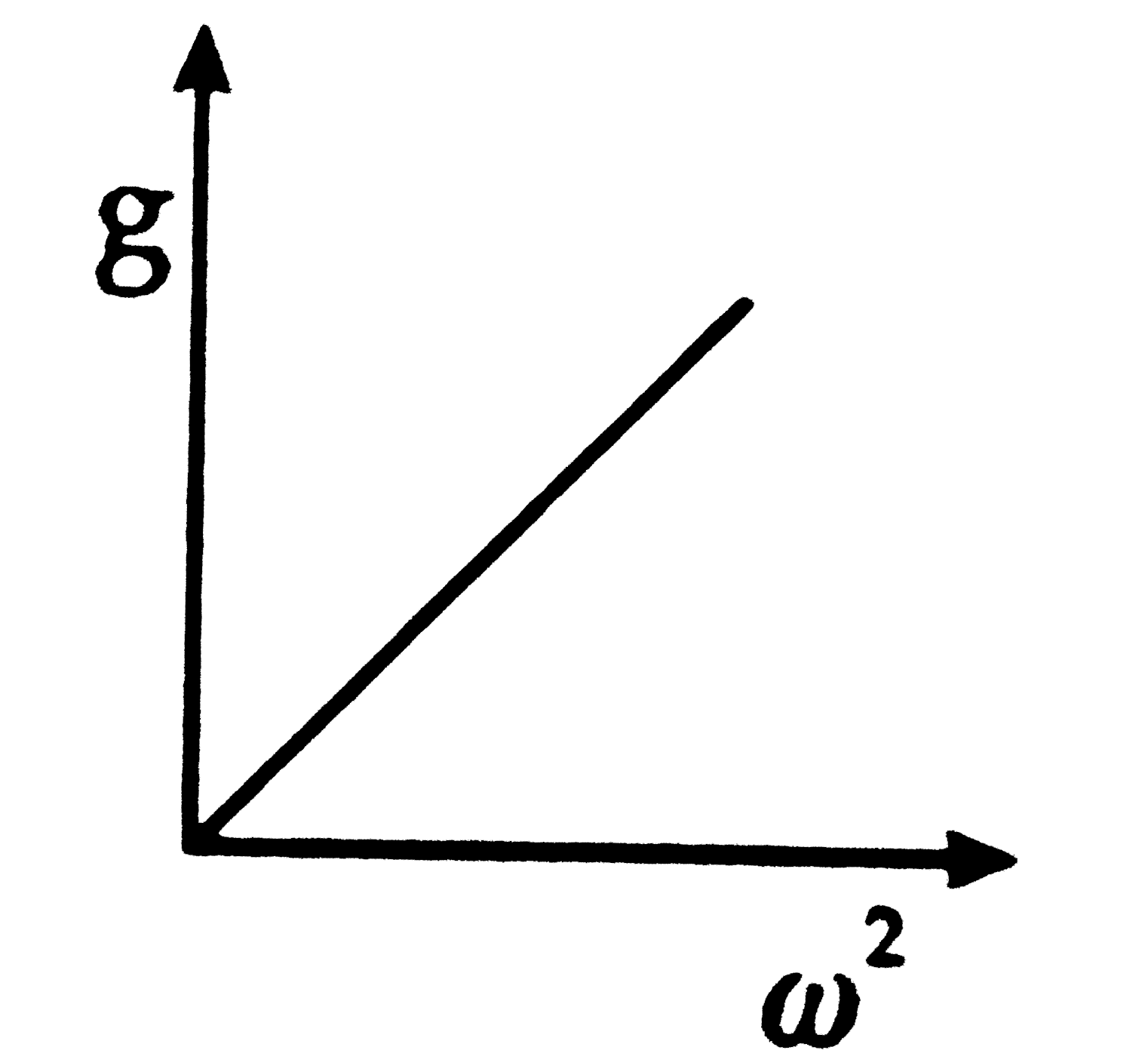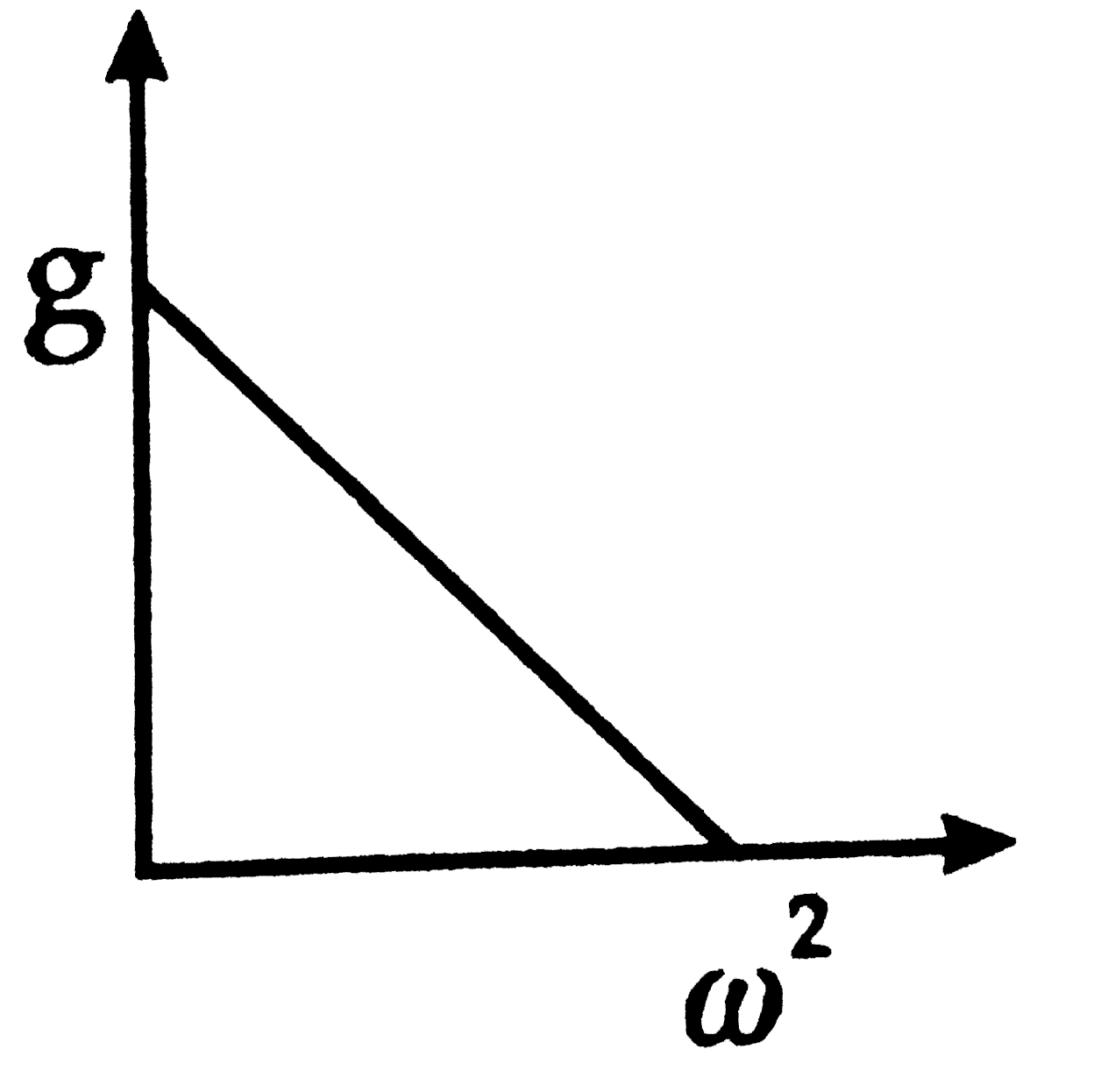A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
ELECTROSTATICS
NIKITA PUBLICATION|Exercise Multiple Choice Questions|458 VideosView PlaylistINTERFERENCE AND DIFFRACTION
NIKITA PUBLICATION|Exercise MULTPLE CHOICE QUESTIONS|333 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
NIKITA PUBLICATION-GRAVITATION-Multiple Choice Questions
- The mass of a body at the centre of the earth is
01:27
|
Play - The graph that represents variation of g with height (h) from the surf...
03:29
|
Play - The graph that represents variation of g with depth (d) from the surfa...
02:14
|
Playing Now - The graph that represents variation of g at the equator with square of...
02:41
|
Play - The graph that represents the relation between orbital velocity (v(0))...
02:19
|
Play - The acceleration due to gravity g on the earth is 9.8m//s^(2). What wo...
03:56
|
Play - If the radius of the earth suddenly decreases to 80% of its present va...
02:06
|
Play - The mass of a planet is (1//10)^("th") that of earth and its diameter ...
04:34
|
Play - If both the mass and radius of the earth decrease by 1% the value of
03:35
|
Play - Assuming that the Earth is a sphere of radius R. At what altiude will ...
02:34
|
Play - A high jumper can jump 2.0 m on the earth With the same effort how hig...
07:09
|
Play - The value of the gravitational acceleration at the height h to be 1% o...
02:37
|
Play - What should be the angular velocity of earth, if the apparent value of...
02:49
|
Play - Is it necessary for the plane of the orbit of a satellite to pass thro...
01:00
|
Play - Gravitation on moon is (1)/(6) th of that on earth. When a balloon fil...
01:38
|
Play - When a falling meteor is at a distance above the earth's surface 3 tim...
02:24
|
Play - The centripetal acceleration of a satellite that circles the earth at ...
04:15
|
Play - If g is acceleration due to gravity at the surface of the earth, then ...
01:54
|
Play - The acceleration due to gravity decreases by Deltag(1) when a body is ...
04:02
|
Play - If g is acceleration due to gravity at the equator when earth were at ...
02:29
|
Play