Home
Class 10
MATHS
In the adjoining figure, point Q is the...

In the adjoining figure, point Q is the point of contact of tangent and circle . If PQ = 12, PR = 8, then find Ps and RS .

Text Solution

Verified by Experts

The correct Answer is:
`:.` PS = 18 units , `:.` RS = 10 units
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    CHETAN PUBLICATION|Exercise Problem Set - 3|16 Videos

  • CIRCLE

    CHETAN PUBLICATION|Exercise Problem Set - 3 (MCQs)|10 Videos

  • CIRCLE

    CHETAN PUBLICATION|Exercise Practice Set - 3.4|7 Videos

  • CHALLENGING QUESTIONS

    CHETAN PUBLICATION|Exercise Mensuration|9 Videos

  • CO-ORDINATE GEOMETRY

    CHETAN PUBLICATION|Exercise ASSIGNMENT-5|11 Videos

Similar Questions

Explore conceptually related problems

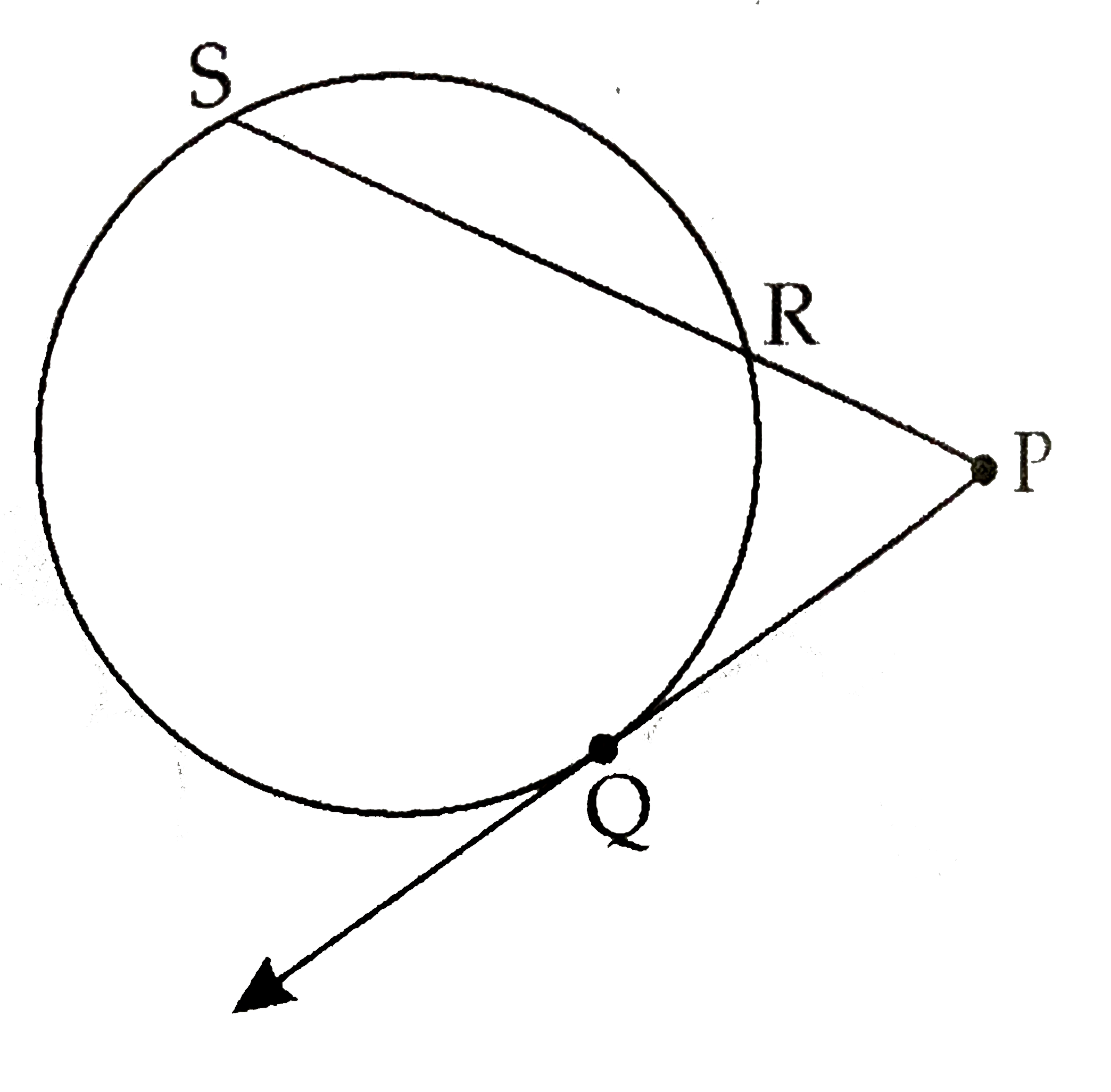
In the adjoining figure, point B is the point of contact and point O is the centre of the circle. Seg OE bot se AD, if AB = 12, AC = 8, then find (i) AD (ii) DC and (iii) DE

In the adjoining figure, ray PQ touches the circle at point Q. Line PRS is a secant, If P=12, PR=8 then PS and RS

In Delta PQR, Point S is the midpoint of side QR. If PQ = 11, PR = 17, PS = 13 then find QR.

In the adjoining figure point O is the centre of the circle . Line PB is a tangent and line PAC is a secnt. Find Paxx PC if OP = 25 and radius is 7 .

In the adjoining figure line PA is tangent at point A . Line PBC is a secant . If AP = 15 and BP = 10 , find BC.

In the adjoining figure, if PQ = 6, QR = 10, PS = 8, then find TS.

In the adjoining figure point A is the centre of the circle . AN = 10 cm . Line NM is tangent at M . MN = 5 cm . Find the radius .

In the adjoining figure, point P is the centre of the circle and line AB is the tangent to the circle at T . The radius of the circle is 6 cm . Find PB if angleTPB=60^(@)

In the adjoining figure, M is the centre of the circle and seg KL is a tangent segment. If MK = 12, KL =6sqrt(3) , then (i) Find radius of the circle. (ii) Find measure of angleK and angleM .

In the adjoining figure, M is the midpoint of QR. anglePRQ = 90^(@) prove that PQ^(2) = 4 PM^(2) - 3 PR^(2)