Gauss's law : The total electric flux through any closed surface is equal to `1/epsi_(0)` times the net charge enclosed by the the surface. i.e., `phi=oint_(S)vec(E).d vec(s)=q/epsi_(0)`.
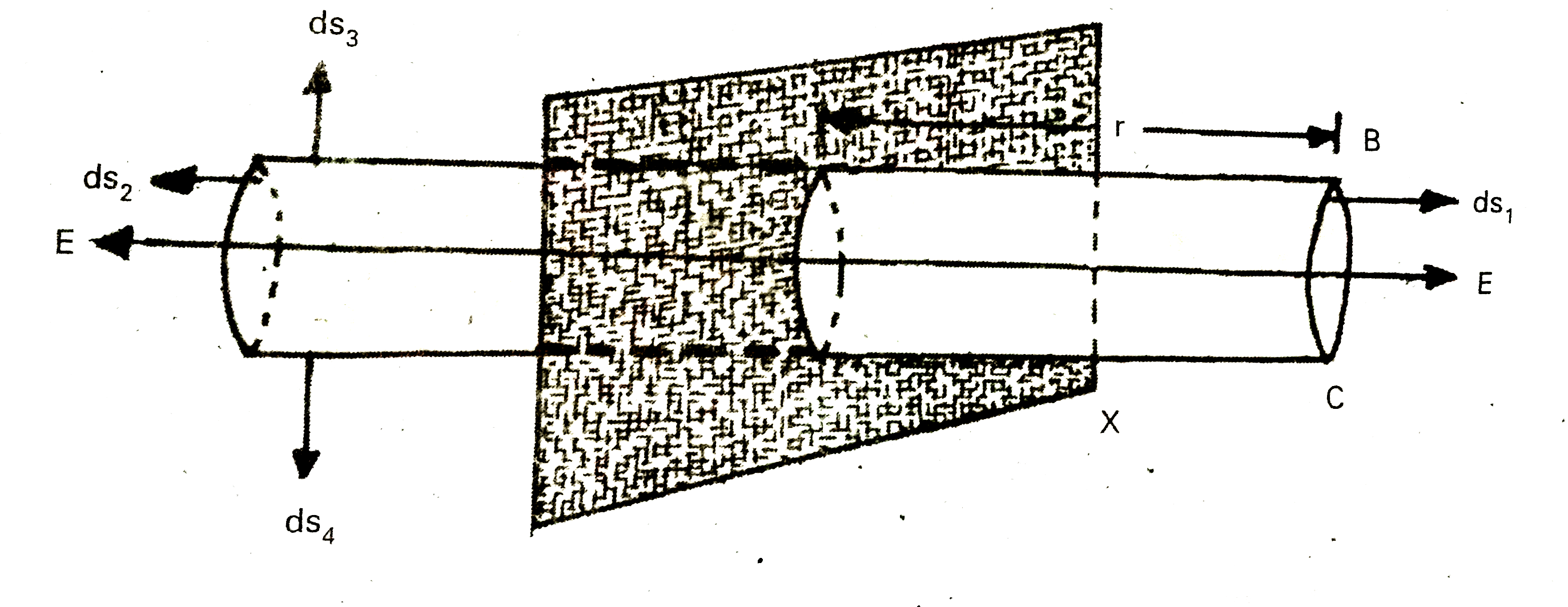
Expression for E due to an infinite plane of charge :
(1) Consider an infinite plane sheet of charge. Let the charge distribution is uniform on this plane.
Uniform charge density on this surface `sigma=(d q)/(d S)` where dq is the charge over an infinite samall area ds.
(3) Construct a horizontal cylindrical Gaussian surface ABCD perpendicular to the plane with length 2r.
(4) The flat surface BC and AD are parallel to the plane sheet and area at equal distance from the plane.
Let area of these surfaces are `dS_(1)` and `dS_(2)`. They are parallel to `vec(E)`. So flux through these two surfaces is `oint_(s)vec(E).d vec(S)=int E dS=E(S+S)=2ES` ...(1)
Where S is area of plane surface AD or BC. Both are equal in area and intensity.
(6) Consider cylindrical surface of AB and CD. Let their areas are say `dS_(3)` and `dS_(4)`. These surfaces are `bot^(lr)` to electric intensity `vec(E)`.
(7) So angle between `vec(E)` and `dvec(S)_(3)` or `dS_(4)` is `90^(@)`. Total flux through these surface is zero. Since `oint_(S)vec(E).d vec(S)=0`.
(8) From Gauss's law total flux, `phi=oint vec(E).d vec(S)=2ES=q/epsi_(0)`
`:. 2ES = (sigma S)/epsi_(0) [ :' Q = sigma xx S]`
(9) Therefore intensity of electric field due to an infinite plane sheet of charge `E=sigma/(2 epsi_(0))`.
