Recommended Questions
- A uniform rod of length l and mass M rotating about a fixed vertical a...
09:25
|
Playing Now - A uniform rod of length L lies on a smooth horizontal table. A particl...
07:35
|
Play - A uniform rod of mass m and length l rotates in a horizontal plane wit...
03:21
|
Play - A thin uniform rod of mass m and length l is kept on a smooth horizont...
06:32
|
Play - A uniform rod of length l and mass M rotating about a fixed vertical a...
09:25
|
Play - Two point masses A of mass M and B of mass of 4M are fixed at the ends...
01:50
|
Play - A uniform rod AB of mass m and length L rotates about a fixed vertical...
02:12
|
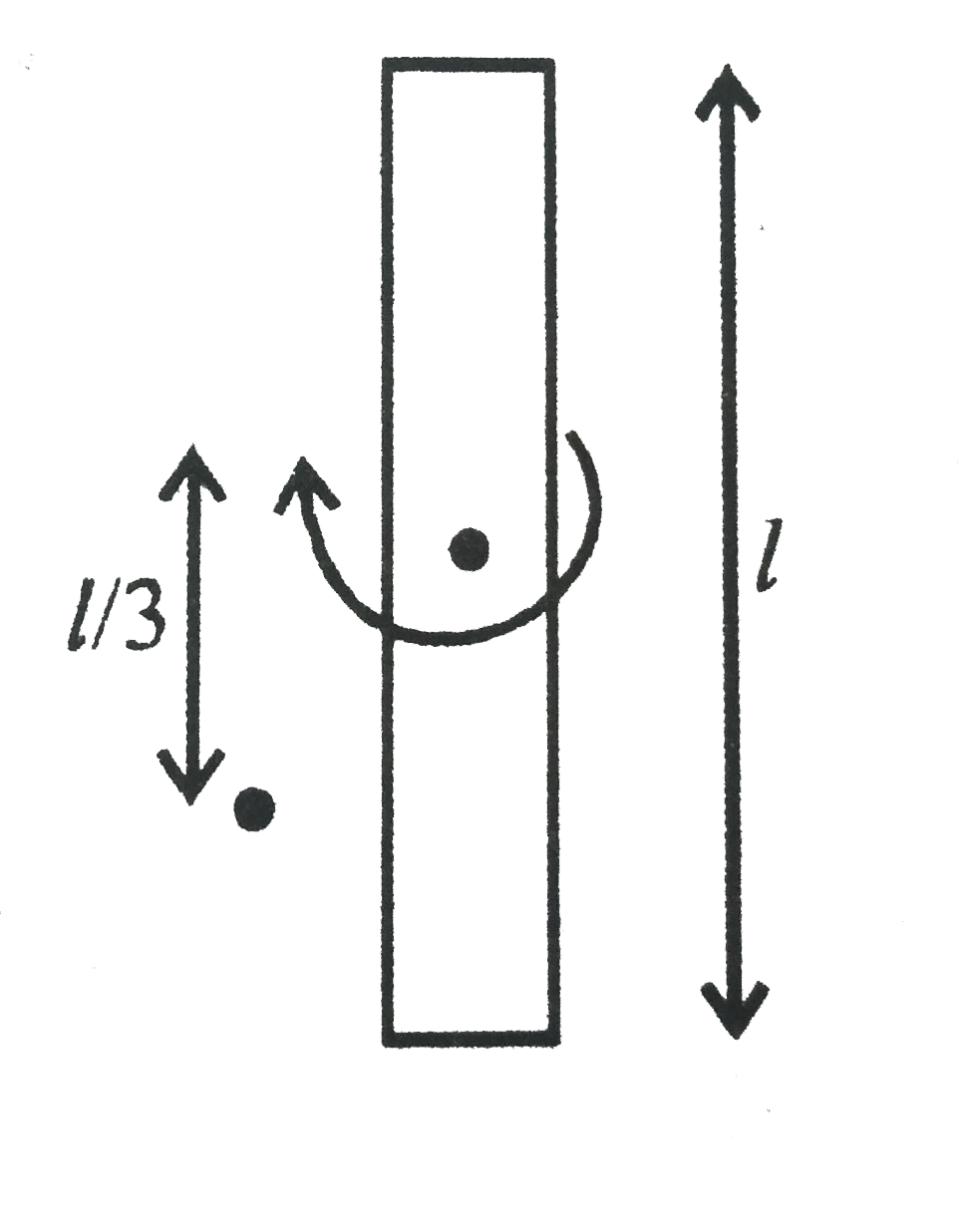
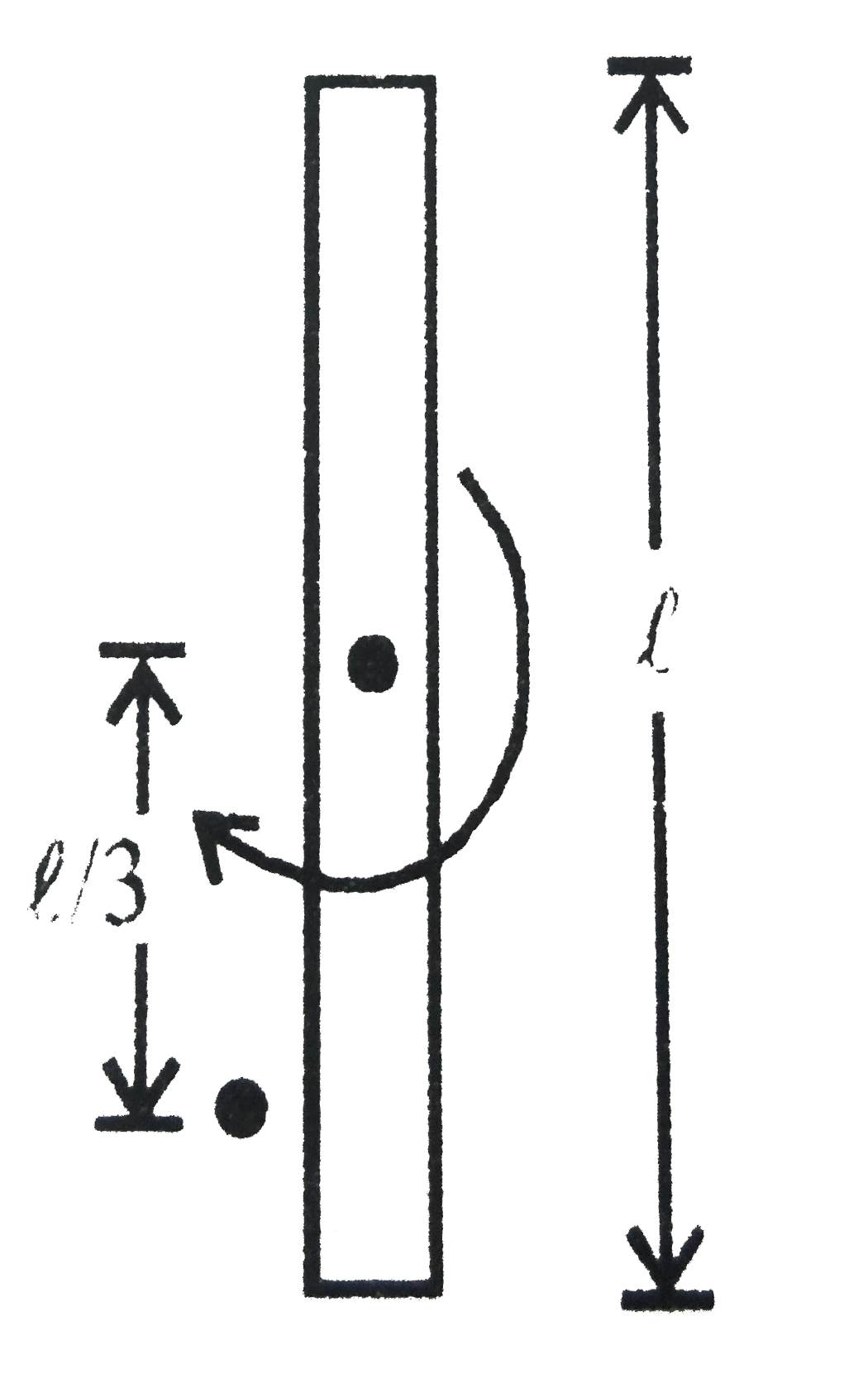
Play - एक पतली छड़ का द्रव्यमान M तथा लम्बाई l है। छड़ के एक सिरे से l//3 दूरी ...
02:46
|
Play - A thin uniform rod of mass 'm' and length 'l' is kept on a smooth hori...
Text Solution
|
Play
 .
. .
.