Recommended Questions
- A uniform circular disc placed on a rough horizontal surface has initi...
Text Solution
|
Playing Now - A uniform circular disc of radius r is placed on a rough horizontal su...
05:00
|
Play - A uniform circular disc placed on a rough horizontal surface has initi...
Text Solution
|
Play - A uniform disc of mass m and radius R is released gentiy on a horizont...
02:32
|
Play - A uniform circular disc placed on a horizontal rough surface has initi...
02:49
|
Play - A uniform circular disc of radius r . 1placed on a rough horizontal pl...
Text Solution
|
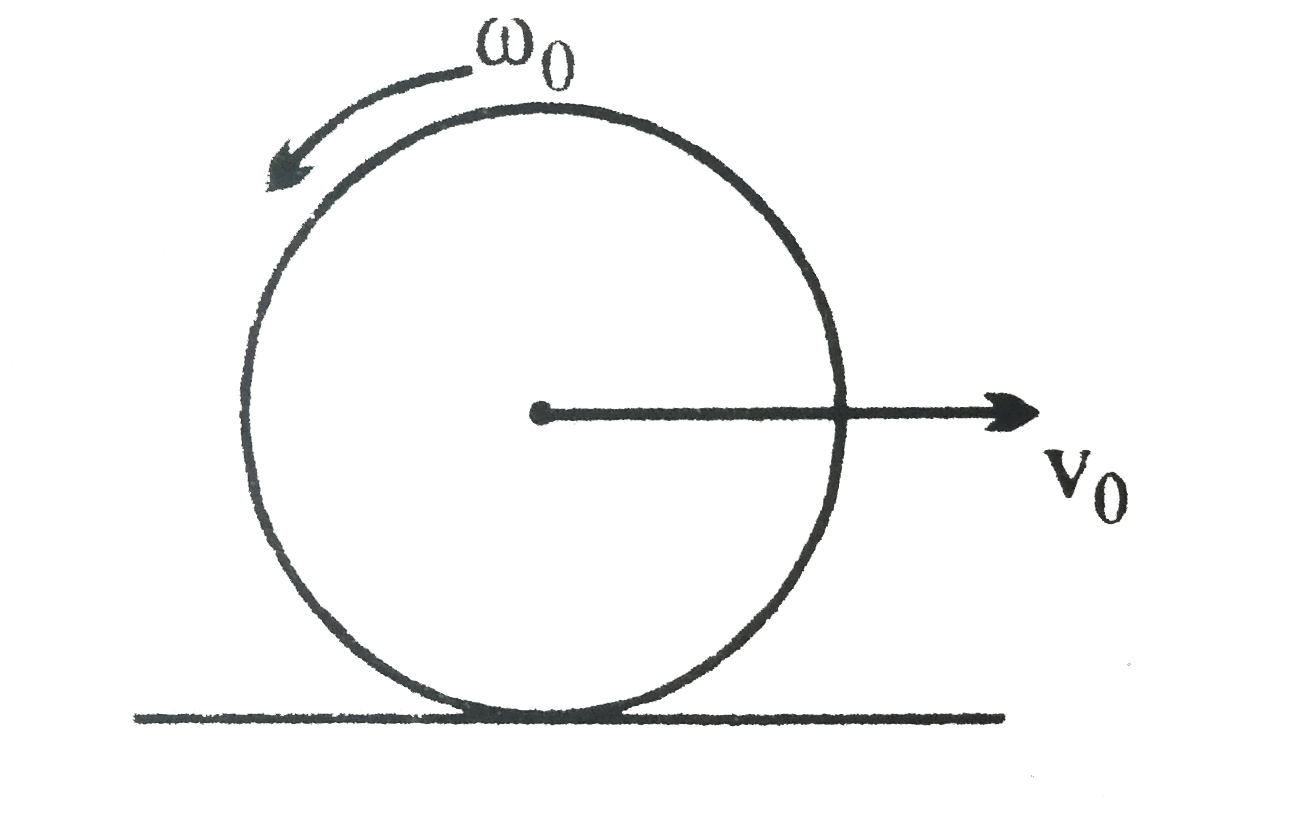
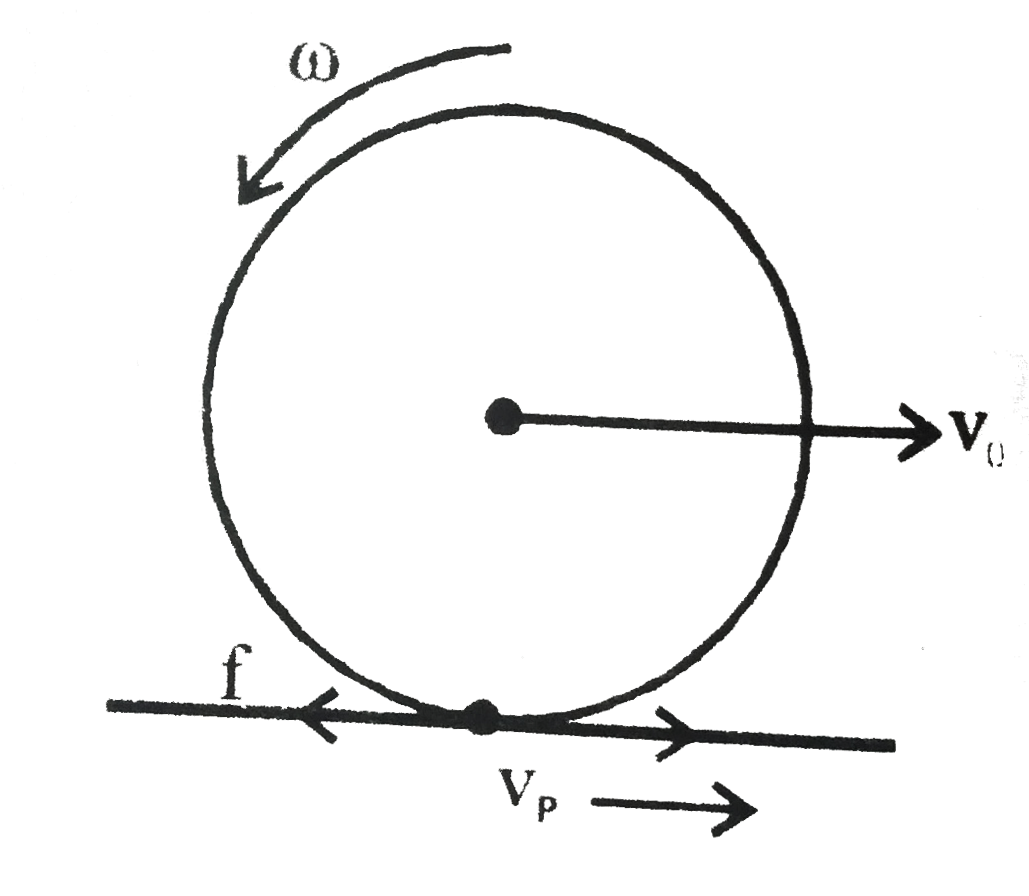
Play - A disc is given an angular velocity omega(0) and a linear velocity v(0...
Text Solution
|
Play - a uniform circular disc of radiu8s r placed on a roughn horizontal pla...
Text Solution
|
Play - In each situation of Table-1, a uniform disc of mass m and radius R ro...
Text Solution
|
Play
 .
. .
.