Text Solution
Verified by Experts
|
Topper's Solved these Questions
ROTATIONAL MOTION
CP SINGH|Exercise Exercise|172 VideosView PlaylistRELATIVE MOTION
CP SINGH|Exercise EXERCISE|33 VideosView PlaylistSIMPLE HARMONIC MOTION
CP SINGH|Exercise Exercises|125 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
CP SINGH-ROTATIONAL MOTION-Exercise
- Three thin unifrom circular discs each of mass M and radius R are plac...
04:12
|
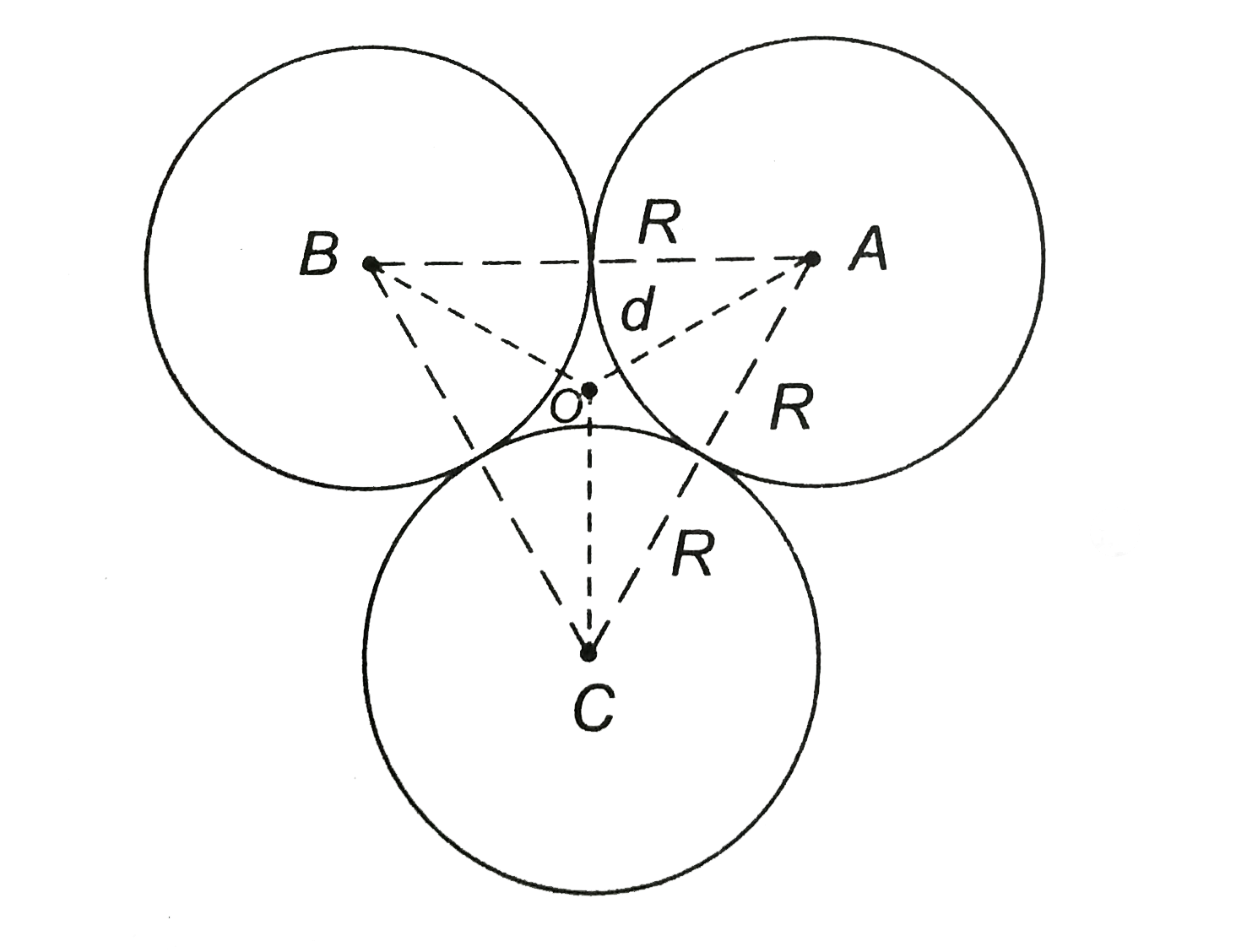
Playing Now - Three point masses, each of mass m, are placed at the corners of an eq...
02:47
|
Play - The moment of inertia of a disc of mass M and radius R about an axis. ...
01:01
|
Play - Let I(A) and I(B) be moments of inertia of a body about two axes A and...
01:35
|
Play - A closed cylindrica tube containing some water (not filling the entire...
02:36
|
Play - A uniform cylinder has radius R and length L. If the moment of inertia...
02:27
|
Play - A solid sphere of mass M, radius R and having moment of inertia about ...
01:40
|
Play - Two circular discs are of same thickness. The diameter of A is twice t...
02:12
|
Play - The moment of inertia of a circular disc of mass M and radius R about ...
03:22
|
Play - From a uniform wire, two circular loops are made (i) P of radius r and...
03:13
|
Play - The moment of inertia of a uniform rod about a perpendicular axis pass...
02:06
|
Play - The density of a rod AB increases linearly from A to B its midpoint is...
04:17
|
Play - The M.I. of a rod about an axis through its center and perpendicular t...
02:47
|
Play - The moment of inertia of a thin uniform rod of mass M and length L abo...
01:05
|
Play - Three rings, each of mass m and radius r, are so placed that they touc...
02:49
|
Play - Two rings A (2m,R) and B (m,R) are placed such that these are perpendi...
02:31
|
Play - If I(0) is the moment of inertia body about an axis passing through it...
01:41
|
Play - A rod of length L is made of a uniform length L//2 of mass M(1) and a ...
03:22
|
Play - Four spheres each of mass M and diameter 2r, are placed with their cen...
04:29
|
Play - The ratio of the radii of gyration of a circular disc about a tangenti...
04:10
|
Play - One quarter sector is cut from a uniform circular disc of radius R. Th...
03:46
|
Play