A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
SYSTEM OF PARTICLES
NARAYNA|Exercise Level-V|72 VideosView PlaylistPHYSICAL WORLD
NARAYNA|Exercise C.U.Q|10 VideosView PlaylistSYSTEM OF PARTICLES AND ROTATIONAL MOTION
NARAYNA|Exercise EXERCISE - IV|39 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
NARAYNA-SYSTEM OF PARTICLES-Level-VI
- The KE and moment of inertia about the given end point of a rod of mas...
03:05
|
Play - The torque tau on a body about a given point is found to be equal to A...
01:44
|
Play - Consider a sphere of mass 'm' radius 'R' doing pure rolling motion on ...
03:10
|
Playing Now - If a cylinder is rolling down the incline with sliding -
02:42
|
Play - which of the following statements are correct.
07:16
|
Play - A small particle of mass m is given an initial velocity v(0) tangent t...
06:15
|
Play - A small particle of mass m is given an initial velocity v(0) tangent t...
06:15
|
Play - A small particle of mass m is given an initial velocity v(0) tangent t...
06:15
|
Play - A rod AB of mass 3m and length 4a is falling freely in a horizontal po...
03:02
|
Play - A rod AB of mass 3m and length 4a is falling freely in a horizontal po...
18:53
|
Play - A rod AB of mass 3m and length 4a is falling freely in a horizontal po...
18:53
|
Play - An uniform rod of mass m=30 kg and length l=0.80 m is free to rotate a...
17:47
|
Play - An uniform rod of mass m=30 kg and length l=0.80 m is free to rotate a...
17:47
|
Play - A uniform thin cylindrical disk of mass M and radius R is attaached to...
04:44
|
Play - A uniform thin cylindrical disk of mass M and radius R is attaached to...
01:33
|
Play - A uniform thin cylindrical disk of mass M and radius R is attaached to...
03:03
|
Play - A wheel of radius R, mass m with an axle of radius r is placed on a ho...
03:47
|
Play - A wheel of radius R, mass m with an axle of radius r is placed on a ho...
03:37
|
Play - A wheel of radius R, mass m with an axle of radius r is placed on a ho...
03:37
|
Play - Consider a cylinder of mass M=1 kg and radius R=1 mlying on a rough ho...
06:08
|
Play

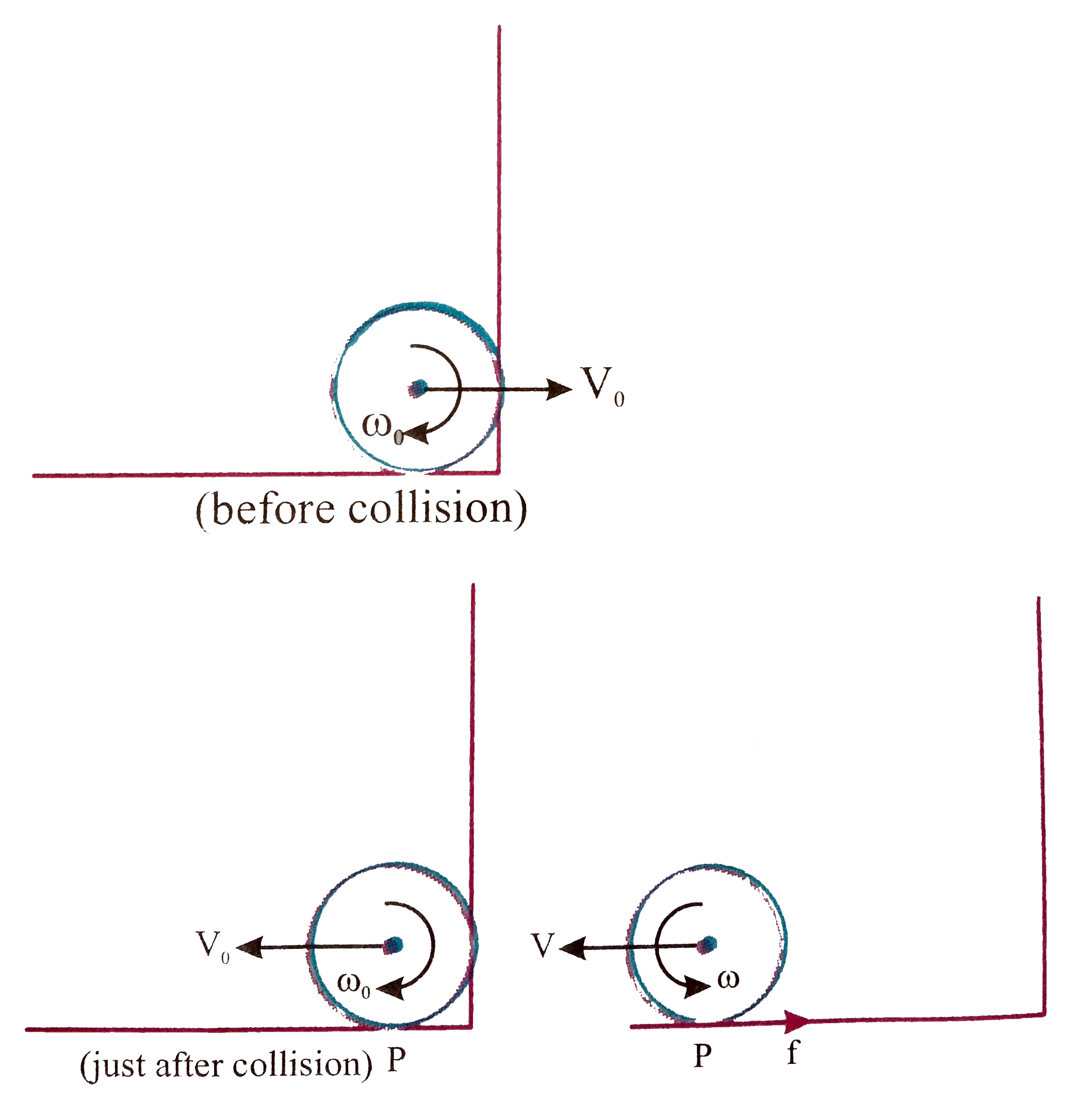 (at the point of pure rolling)
(at the point of pure rolling)