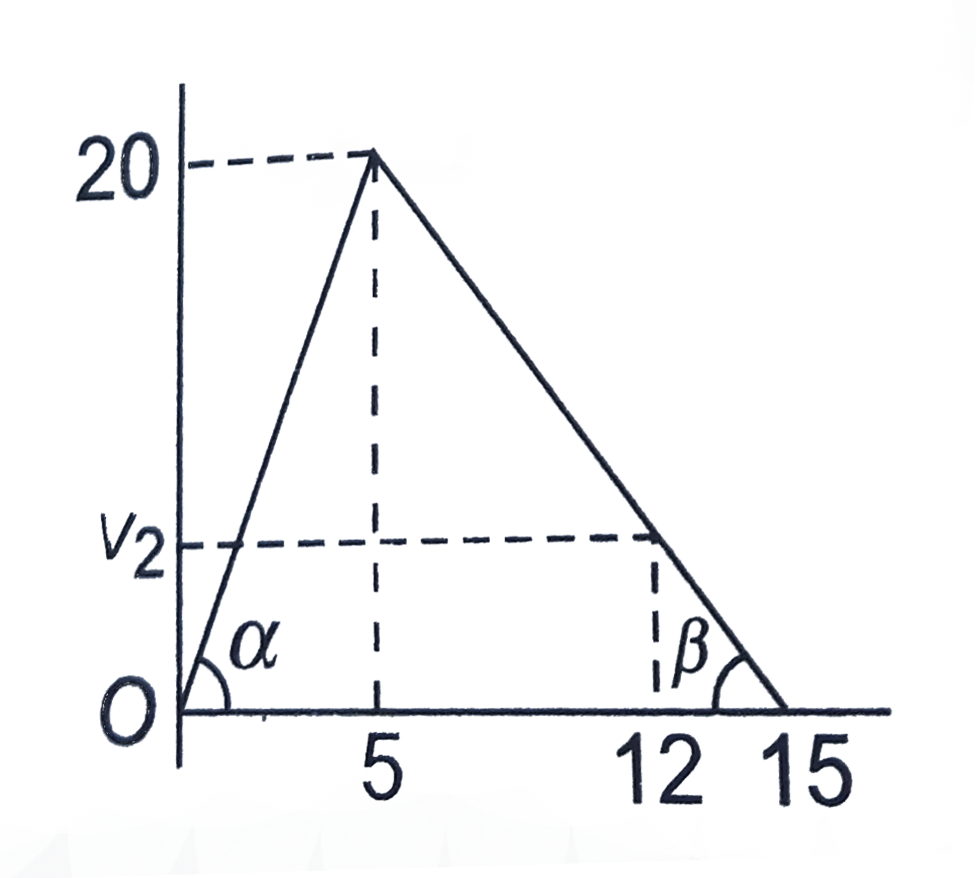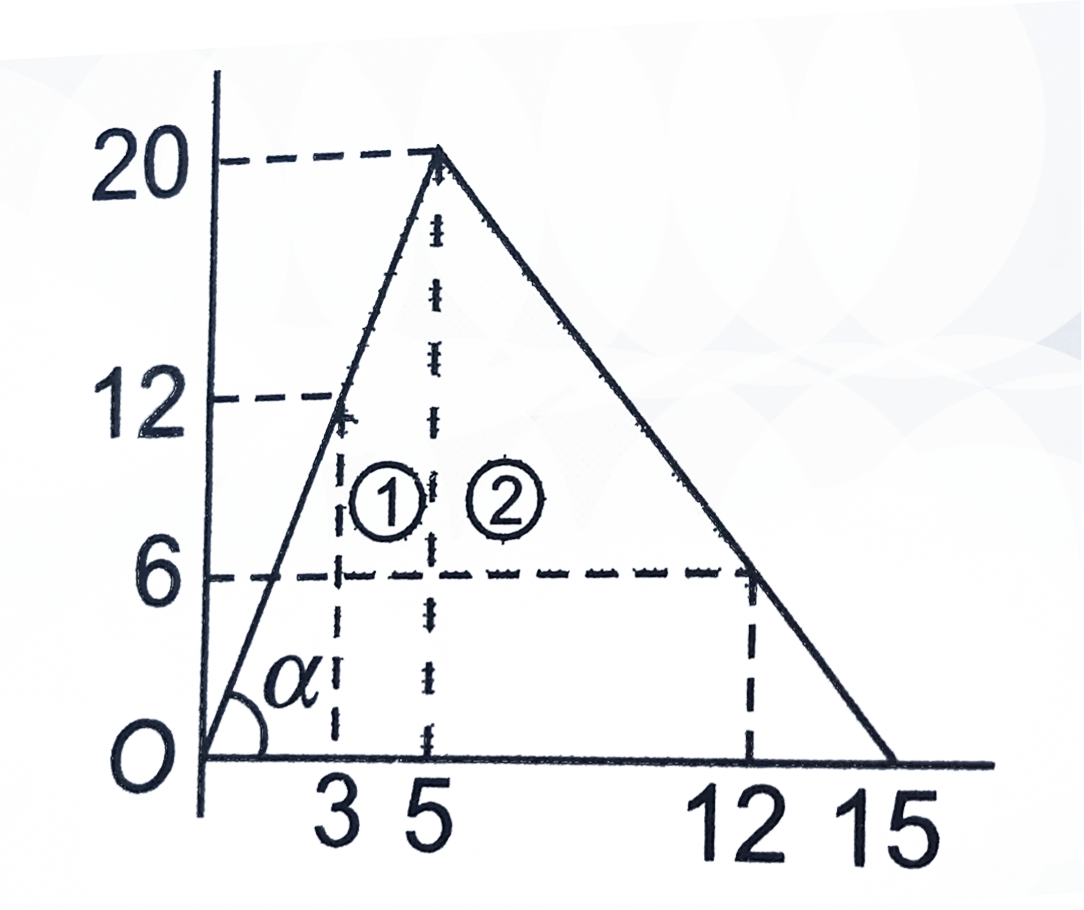Text Solution
Verified by Experts
|
Topper's Solved these Questions
MOTION IN A STRAIGHT LINE
CP SINGH|Exercise EXERCISES|128 VideosView PlaylistMOTION IN A PLANE
CP SINGH|Exercise Exercises|69 VideosView PlaylistNEET PREVIOUS YEAR
CP SINGH|Exercise Solved Questions|64 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
CP SINGH-MOTION IN A STRAIGHT LINE-EXERCISES
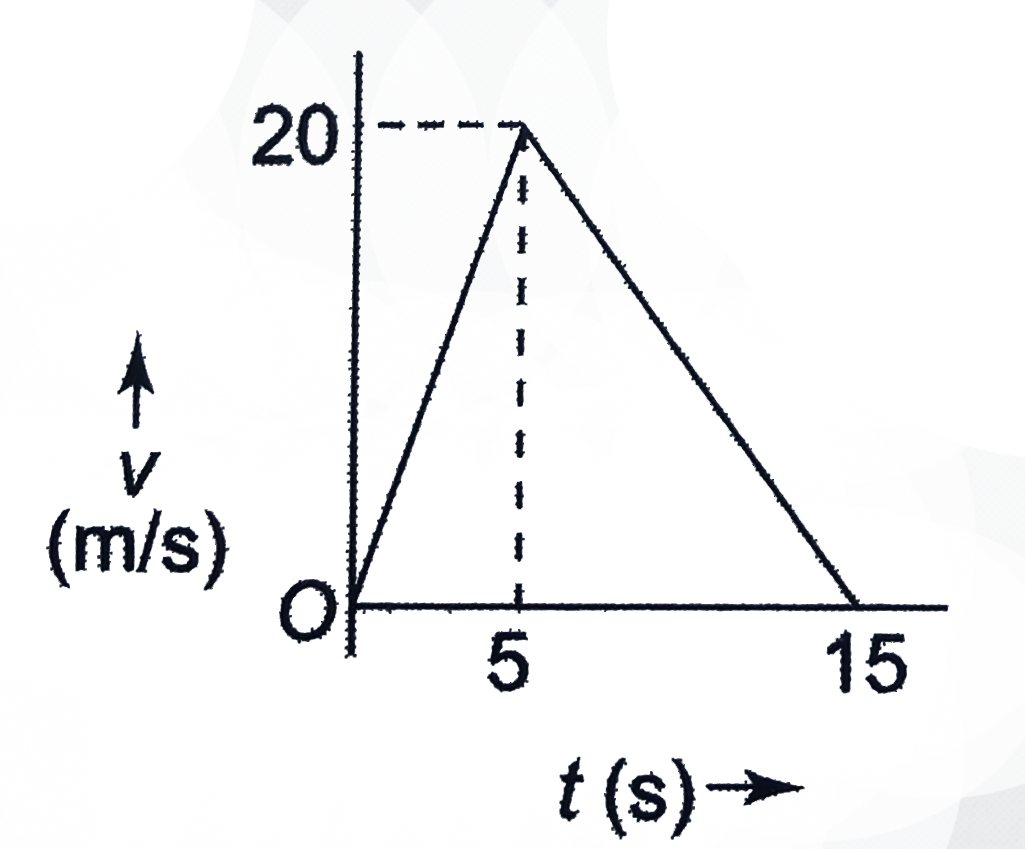
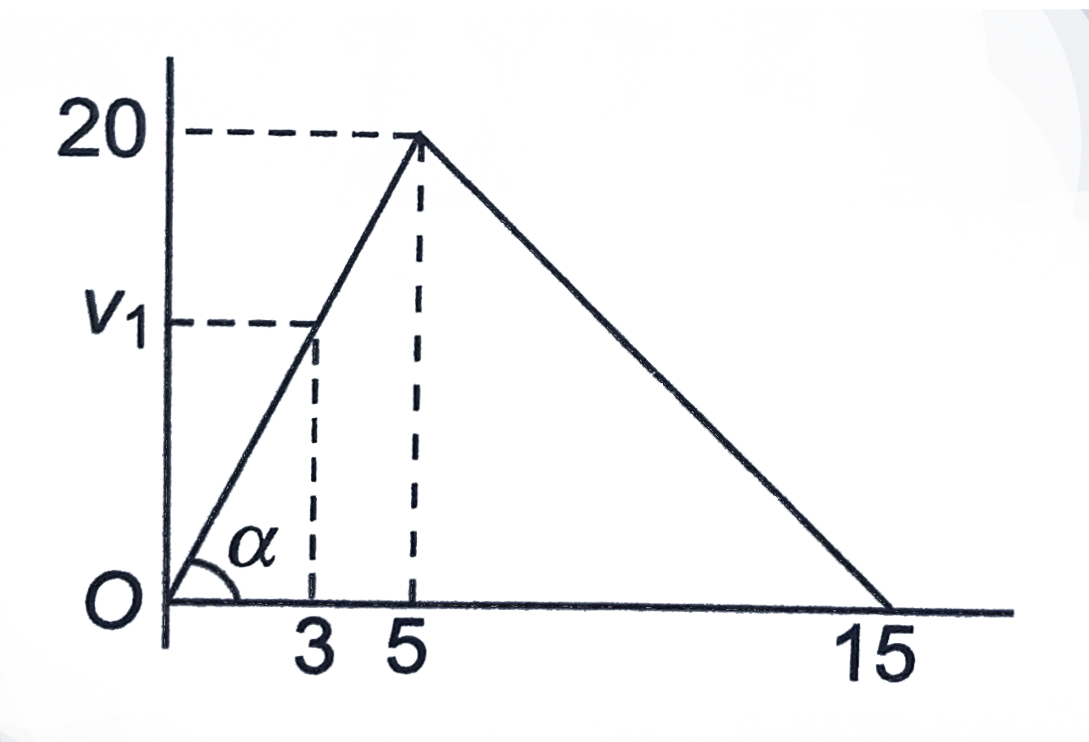
- From the following v-t graph, find the displacement for time interval ...
04:38
|
Playing Now - The ratio of the numerical values of the average velocity and average ...
01:33
|
Play - Which of the following is a one-dimensional motion ?
01:08
|
Play - A point traversed half a circle of radius r during a time interval t(0...
01:56
|
Play - A particle moves 3 m north, then 4 m east, and then 12 m vertically up...
02:20
|
Play - A person travelling on a straight line moves with a uniform velocity v...
01:55
|
Play - A car moves from X to Y with a uniform speed vu and returns to Y with ...
02:58
|
Play - A particle moves in a straight line from A to B (a) for the first ha...
05:48
|
Play - If a car covers (2)/(5)^(th) of the total distance with v1 speed and (...
02:26
|
Play - A car travels half the distance with a constant velocity of 40 m//s an...
02:11
|
Play - One car moving on a staright road covers one-third of the distance wit...
02:09
|
Play - A particle moving in a straight line covers half the distance with spe...
04:07
|
Play - A body starts from rest. What is the retio of the distance traveled by...
01:38
|
Play - A partical is moving in a straight line under constant acceletation. I...
02:05
|
Play - A particle is moving in a straight line under constant acceleration of...
02:07
|
Play - A body is moving with a uniform acceleration coverss 40 m in the first...
02:02
|
Play - A particle starts its motion from rest under the action of a constant ...
02:25
|
Play - A body travels for 15 s starting from rest with a constant acceleratio...
04:22
|
Play - A body moving with a uniform acceleration crosses a distance of 15 m i...
04:58
|
Play - A 150 m long train is moving with a uniform velocity of 45 km//h. The ...
02:52
|
Play - Speeds of two identical cars are u and 4u at at specific instant. The ...
06:48
|
Play