Home
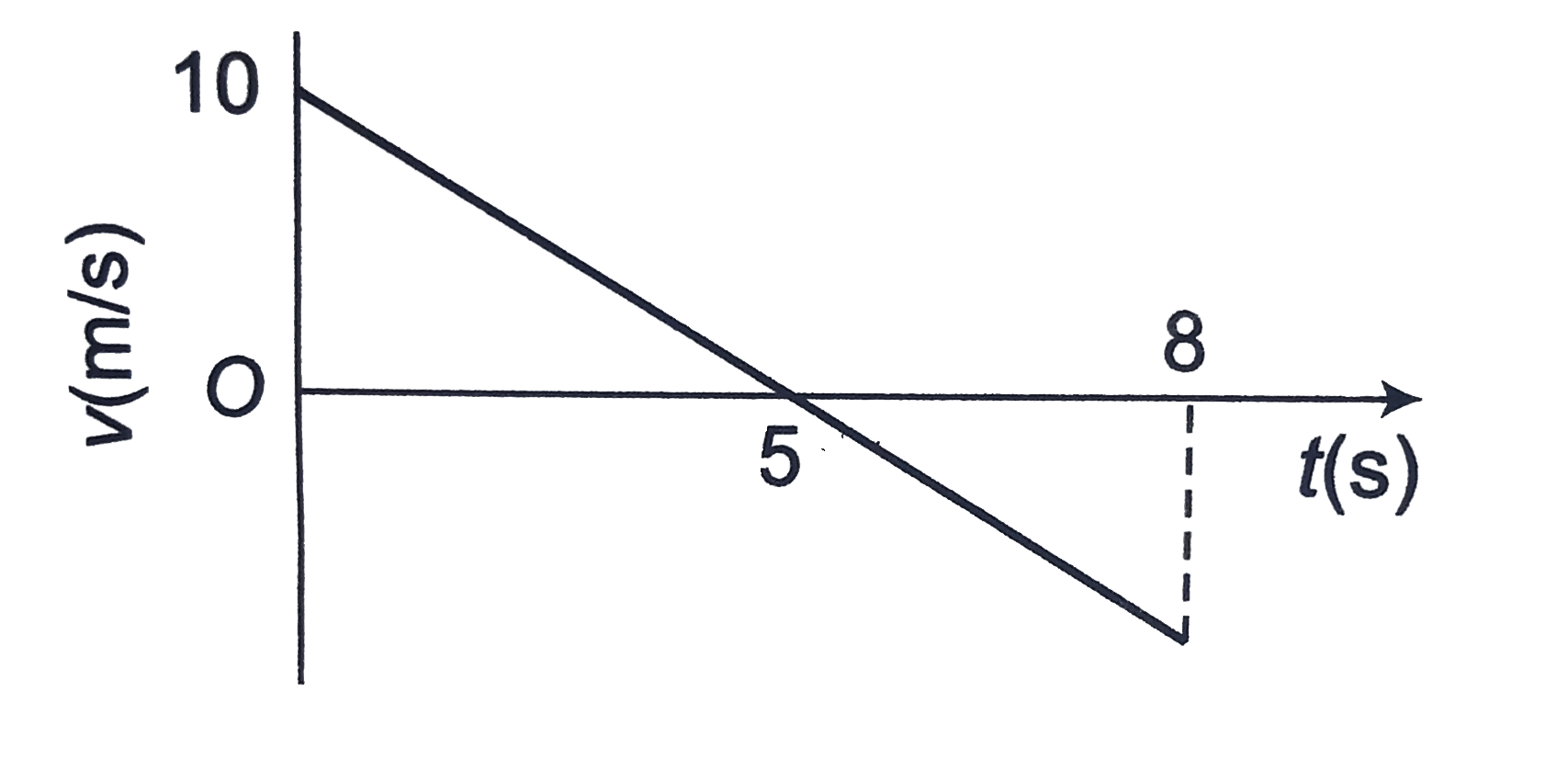
Class 11
PHYSICS
At the moment t=0 particle leaves the or...

At the moment t=0 particle leaves the origin and moves in the positive direction of the x-axis. Its velocity varies with time as `v=10(1-t//5)`. The dislpacement and distance in 8 second will be

A

16 m, 34 m

B

16 m, 25 m

C

16 m, 16 m

D

16 m, 9m

Text Solution

Verified by Experts

The correct Answer is:
A
`v=10(1-t/5)=10-2t`
`(ds)/dt =10-2t`
`int_(0)^(s) ds=int_(0)^(8)(10-2t)dt`
`s=10t-2t^(2)/2=|10t=t^(2)|_(0)^(8)`
`=10(8)-(8)^(2)=80-64=16 m`
Displacement`=16 m`
To find the distance, first determine whether velocity becomes zero in the given time interval or not.
`v=10-2t=0impliest=5 s`

Distance`=int_(0)^(5) v dt+|int_(5)^(8) v dt|`
`=25+|-9|=25+9=34 m`
OR
Draw a v-t graph

Area of v-t graph gives displacement and distance
Displacement`=25-9=16 m`
Distance`=25+9=34 m`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • MOTION IN A STRAIGHT LINE

    CP SINGH|Exercise EXERCISES|128 Videos

  • MOTION IN A PLANE

    CP SINGH|Exercise Exercises|69 Videos

  • NEET PREVIOUS YEAR

    CP SINGH|Exercise Solved Questions|64 Videos

Similar Questions

Explore conceptually related problems

At the moment t=0 a particle leaves the origin and moves in the positive direction of the x-axis. Its velocity varies with time as v=v_0(1-t//tau) , where v_0 is the initial velocity vector whose modulus equals v_0=10.0cm//s , tau=5.0s . Find: (a) the x coordinate of the particle at the moments of time 6.0 , 10 , and 20s , (b) the moments of time when the particles is at the distance 10.0cm from the origion, (c) the distance s covered by the particle during the first 4.0 and 8.0s , draw the approximate plot s(t) .

(a) At the moment t=0 , a particle leaves the origin and moves in the positive direction of the x-axis. Its velocity is given by v=10-2t . Find the displacement and distance in the first 8s . (b) If v=t-t^(2) , find the displacement and distamce in first 2s.

Knowledge Check

  • A particle located at x = 0 at time t = 0 , starts moving along with the positive x-direction with a velocity 'v' that varies as v = a sqrt(x) . The displacement of the particle varies with time as

    A
    ` t^(2)`
    B
    `t`
    C
    `t^(1/2)`
    D
    `t^(3)`

  • The velocity of a particle moving in the positive direction of x-axis veries as v=10sqrtx . Assuming that at t=0 , particle was at x=0

    A
    The initial velocity of the particle is zero
    B
    the initial velocity of the particle is `2.5(m)/(s)`.
    C
    The accelration of the particle is `2.5(m)/(s^2)`.
    D
    The acceleration of the particle is `50(m)/(s^2)`.

  • A particle located at x = 0 at time t = 0, starts moving along the positive x-direction with a velocity that varies as v=psqrtx . The displacement of the particle varies with time as (where, p is constant)

    A
    `t^(3)`
    B
    `t^(2)`
    C
    `t`
    D
    `t^(1//2)`

    • Similar Questions

    Explore conceptually related problems

    At the moment t=0 a particle leaves the origin and moves in the positive direction of the x-axis.Its velocity at any time is vecv=vecv_0(1-t/tau) where v_0=10 cm/s and tau =5 s. Find : (a)the x-coordinates of the particle at the instant 6s, 10s and 20s. (b)the instant at which it is a distance 10 cm from the origin. (c )the distance s covered by the particle during the first 4s and 8s.

    Acceleration of particle moving along the x-axis varies according to the law a=-2v , where a is in m//s^(2) and v is in m//s . At the instant t=0 , the particle passes the origin with a velocity of 2 m//s moving in the positive x-direction. (a) Find its velocity v as function of time t. (b) Find its position x as function of time t. (c) Find its velocity v as function of its position coordinates. (d) find the maximum distance it can go away from the origin. (e) Will it reach the above-mentioned maximum distance?

    A particle located at "x=0" at time "t=0" starts moving along the positive "x" - direction with a velocity "v" that varies as "v=alpha sqrt(x)".The displacement "(x)" of the particle varies with time as "(alpha" is constant)

    The velocity of a particle moving in the positive direction of the X-axis varies as V=Ksqrt(S) where K is a positive constant. Draw V-t graph.

    Acceleration of a particle moving along the x-axis is defined by the law a=-4x , where a is in m//s^(2) and x is in meters. At the instant t=0 , the particle passes the origin with a velocity of 2 m//s moving in the positive x-direction. (a) Find its velocity v as function of its position coordinates. (b) find its position x as function of time t. (c) Find the maximum distance it can go away from the origin.

    Home
    Profile